A94843.Maple 与树之美 (简单版)

这是该题目的简单版本。本版本与其它版本的区别在于本版本中 $t$ 和 $n$ 的数据范围更小。只有在你解决了所有版本的本题后，才能 hack 其他人。

Maple 得到了一棵有根树，这棵树有 $n$ 个顶点，编号为 $1$ 到 $n$，根节点编号为 $1$。树上每个顶点都被标记为 $0$ 或 $1$。遗憾的是，Maple 忘记了各个顶点的具体标记，但他只记得正好有 $k$ 个节点被标记为 $0$，其余 $n-k$ 个节点被标记为 $1$。

对于每一个顶点，我们将其“名称”定义为一串二进制字符串，该字符串将从根节点到该节点路径上，所有节点的标记顺次拼接而成。更正式地，记 $\text{name}_1 = \text{label}_1$，对于所有 $2\le u\le n$，有 $\text{name}_u = \text{name}_{p_u} + \text{label}_u$，其中 $p_u$ 是顶点 $u$ 的父节点，$+$ 表示字符串拼接。

这棵树的美丽值被定义为所有叶子节点的名称的最长公共子序列的长度。

你的任务是，在所有标记方案中，恰好有 $k$ 个 $0$ 和 $n-k$ 个 $1$，求最大可能的美丽值。

注：

1. 一个序列 $a$ 是序列 $b$ 的子序列，如果可以通过从 $b$ 的若干（可能是零个或所有）位置任意删除一些元素得到 $a$。字符串 $s_1, s_2, \ldots, s_m$ 的最长公共子序列是能同时作为所有 $s_1, s_2, \ldots, s_m$ 子序列的最长字符串。
2. 叶子结点是指没有子节点的任何顶点。

每组测试包含多个测试用例。第一行一个整数 $t$（$1 \le t \le 50$），表示测试用例数量。

每个测试用例的第一行包含两个整数 $n$ 和 $k$（$2 \leq n \leq 1000$，$0 \leq k \leq n$），分别表示节点数和被标记为 $0$ 的节点数。

第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$（$1 \leq p_i \le i-1$），表示节点 $i$ 的父节点编号。

注意，对所有测试用例 $n$ 的总和没有限制。

对于每个测试用例，输出一个整数，表示在恰好用 $k$ 个 $0$ 和 $n-k$ 个 $1$ 标记结点的所有方案中，能得到的最大美丽值。

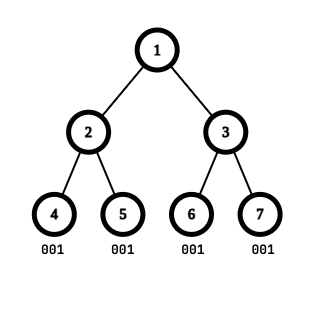
在第一个测试用例中，最大美丽值为 $3$，此时各节点标记为 $[0, 0, 0, 1, 1, 1, 1]$，最长公共子序列为 $001$。

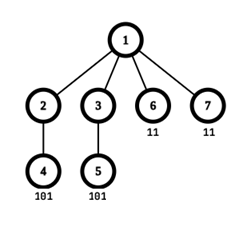
在第二个测试用例中，最大美丽值为 $2$，此时各节点标记为 $[1, 0, 0, 1, 1, 1, 1]$，最长公共子序列为 $11$。