A85852.「COCI 2014.12」MRAVI

译自 COCI 2014/2015 Contest #4 T4「MRAVI」

小 Bobi 每天起床后的首要任务是给他的宠物蚂蚁喂食。

他把它们放在一个玻璃容器里，里面是一个管道系统，可以用一棵有 $N$ 个结点且根节点为 $1$ 的树表示，每条管道对应树中的边。
在这个系统中，液体从某个结点流向这个结点的儿子。

我们知道每条管道的流量 $X_i$，即从父亲结点经过这条管道流到儿子结点的液体百分比。
让我们来研究一下这个例子：

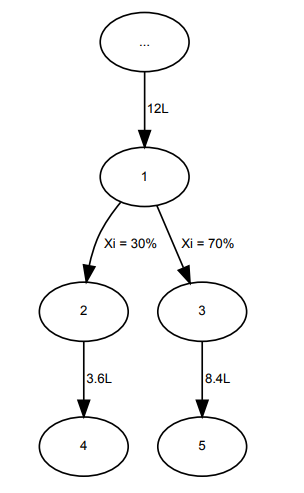
图中，结点 $1$ 有着 $12$ 升液体和两条管道连接。其中一条管道 $X_i = 30$，另一条 $X_i = 70$。
那么，结点 $2$ 将会获得 $3.6$ 升液体，结点 $3$ 将会获得 $8.4$ 升液体。
在给定的数据中，保证一个结点连接的所有管道的 $X_i$ 之和为 $100$。

不过，Bobi 有些管道开了挂，可以让流经的液体变成原来的平方。
比如，如果上述第一条管道开了挂，那么结点 $2$ 获得的液体将会变成 $12.96$ 升，但结点 $3$ 获得的液体仍是 $8.4$ 升。
这个挂的神奇之处在于，一个结点流出的液体可能大于流进这个结点的液体！

蚂蚁只住在叶子结点上。对于每个叶子结点，给定该结点的蚂蚁所需的液体量 $K_i$。Bobi 将会往根结点倒入 $L$ 升液体。
Bobi 想知道，他至少要倒入多少升液体，才能喂饱所有蚂蚁，即求满足条件的最小的 $L$。

数据保证 $L$ 不超过 $2 \cdot 10^9$。

第一行，一个整数 $N$。
接下来 $N-1$ 行，每行四个整数 $A_i,B_i,X_i,T_i$，表示有一条连接 $A_i,B_i$ 的管道，流量为 $X_i$，开挂情况为 $T_i$，为 $1$ 时开挂否则不开。
接下来一行，$N$ 个整数 $K_i$，表示每个结点的蚂蚁所需的液体量。如果第 $i$ 个结点不是叶子，$K_i = -1$。

一行，最小的 $L$。
误差最多为 $0.001$。

$1 \le A_i,B_i \le N \le 1000,1 \le X_i \le 100,0 \le T_i \le 1$。