A75098.闭路

给定一个由 $n$ 个顶点和 $n-1$ 条边组成的连通无向图。每个顶点依次编号为 $1$ 到 $n$。

在图论中，满足这些条件的图被称为树，它具有不含环的性质。
现在，我们考虑向这个图中添加一条原图中不存在的边 $(a,b)$。添加后，图中将恰好形成一个环。
你的任务是，对于给定的若干条待添加的边，输出每条边添加后所形成的环的长度（环所包含的边的数量）。
总共会给出 $Q$ 个待添加的边的询问，你需要对所有这些询问输出答案。

第 $1$ 行是一个整数 $N\ (1 \le N \le 100,000)$，表示图的顶点数。
接下来的 $N-1$ 行描述了图的边。第 $i$ 行包含两个由空格分隔的整数 $x_i$ 和 $y_i$，表示一条连接顶点 $x_i$ 和 $y_i$ 的边。
第 $N+1$ 行是一个整数 $Q\ (1 \le Q \le 100,000)$，表示待添加边的询问数量。
接下来的 $Q$ 行描述了待添加边的信息。第 $i$ 行包含两个由空格分隔的整数 $a_i$ 和 $b_i$，表示第 $i$ 个询问中要添加的边。
保证给定的所有边都连接图中存在的顶点。

• 图不包含自环，即对于任意 $i$，都有 $x_i \neq y_i$。
• 图不包含重边，即对于任意 $i, j (i \neq j)$，都有 $\{x_i, y_i\} \neq \{x_j, y_j\}$。
• 保证待添加的边是原图中不存在的边，并且不是自环。

对于每个询问，输出将该边添加到原图中后形成的环的长度。共输出 $Q$ 行，每行一个答案。请在输出的末尾添加一个换行符。

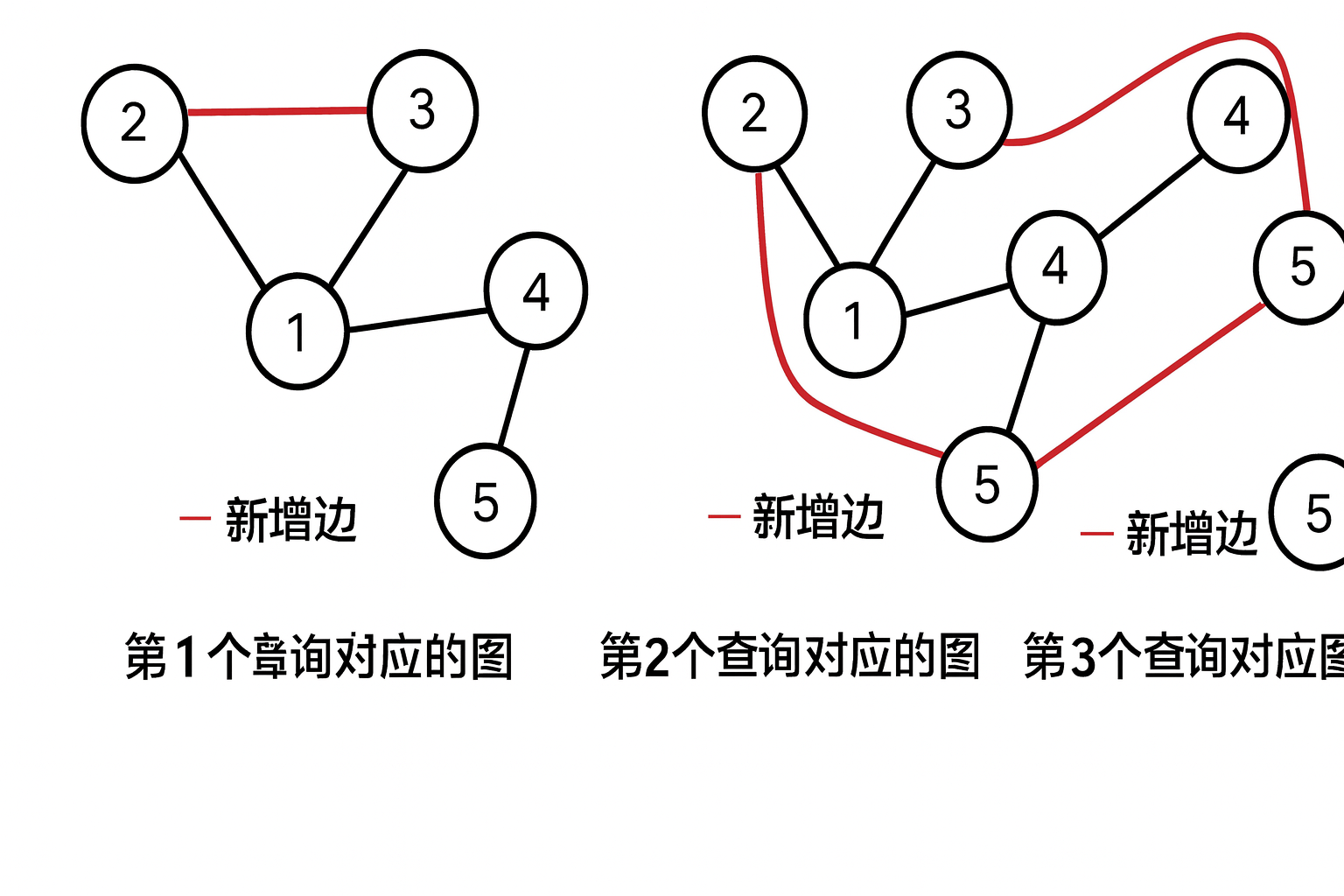
下图展示了样例1中的树结构。