A59728.[NOI2025] 数字树

给定一棵 $4n - 1$ 个结点的二叉树，其中每个非叶结点都有 恰好 两个子结点。非叶结点编号为 $1$ 到 $2n - 1$，叶子结点编号为 $2n$ 到 $4n - 1$。初始时，每个叶子结点上都没有数字。

定义一个 DFS 序是 优美的，当且仅当按该 DFS 序将 所有标有数字的叶子结点 上的数字拼成一个序列时，该序列可以通过若干次 消除相邻相同数字 的方式得到空序列。例如，在下图中，若叶子结点 $4, 6$ 上标有数字 $1$，叶子结点 $5, 7$ 上标有数字 $2$，则按 DFS 序 $[1, 4, 2, 7, 3, 5, 6]$ 将所有标有数字的叶子结点上的数字拼成的序列为 $[1, 2, 2, 1]$，可以通过消除相邻的 $2$ 的方式得到 $[1, 1]$，再通过消除相邻的 $1$ 的方式得到空序列，因此该 DFS 序是优美的；而按 DFS 序 $[1, 4, 2, 3, 5, 6, 7]$ 将所有标有数字的叶子结点上的数字拼成的序列为 $[1, 2, 1, 2]$，无法通过若干次消除相邻相同数字的方式得到空序列，因此该 DFS 序不是优美的。

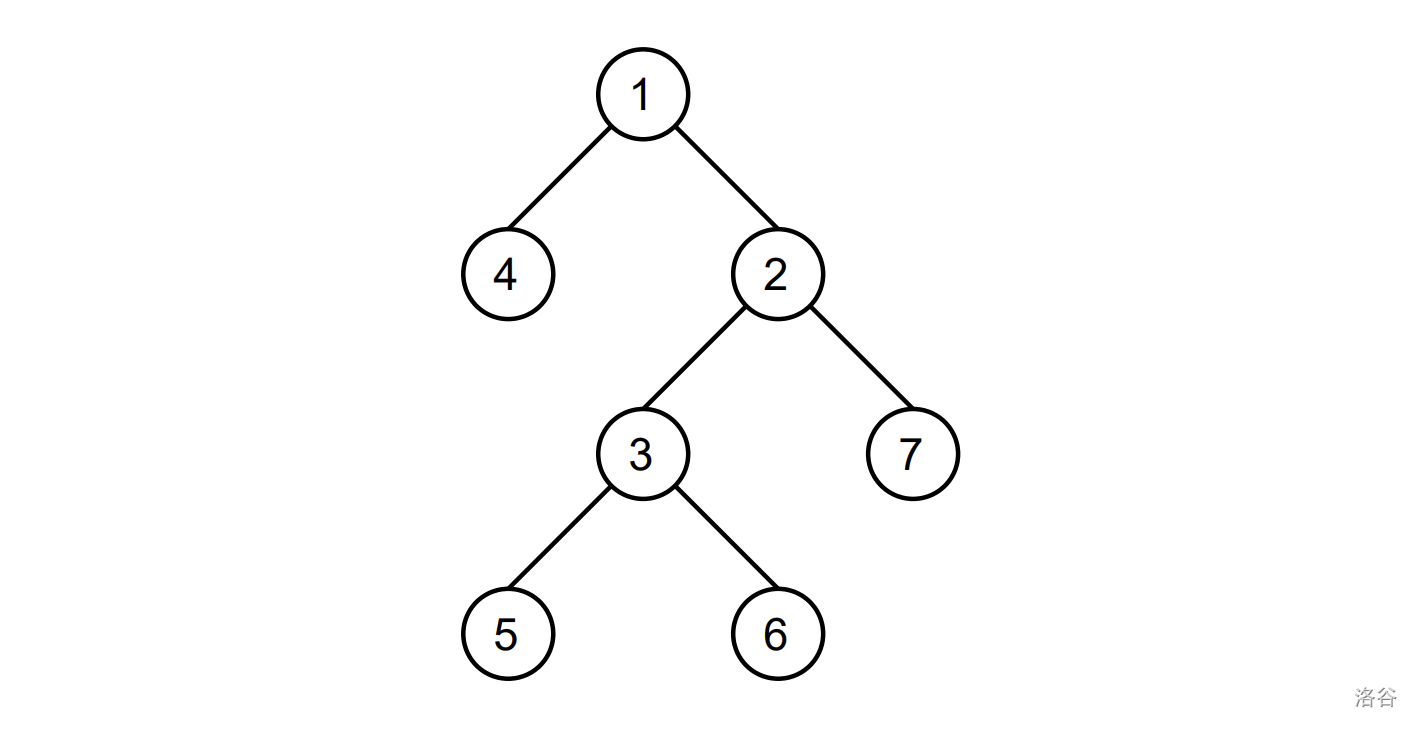
给定 $n$ 次操作，第 $i$ ($1 \leq i \leq n$) 次操作会选择两个 没有数字 的叶子结点，然后将这两个结点标上数字 $i$。保证在每次操作后，存在至少一个优美的 DFS 序。你需要求出每次操作后的优美的 DFS 序的数量。由于答案可能较大，你只需要求出答案对 $1,000,000,007$ 取模后的结果。

输入的第一行包含一个非负整数 $c$，表示测试点编号。$c = 0$ 表示该测试点为样例。

输入的第二行包含一个正整数 $n$，表示二叉树的结点个数为 $4n - 1$。

输入的第 $i + 2$ ($1 \leq i \leq 2n - 1$) 行包含两个正整数 $l_i$ 和 $r_i$，分别表示结点 $i$ 的左右子结点。保证 $i < l_i, r_i \leq 4n - 1$，且所有的 $l_i, r_i$ 互不相同。

输入的第 $i + 2n - 1$ ($1 \leq i \leq n$) 行包含两个正整数 $a_i, b_i$，表示第 $i$ 次操作选择的叶子结点的编号。保证 $2n \leq a_i, b_i \leq 4n - 1$，且所有的 $a_i, b_i$ 互不相同。

输出 $n$ 行，其中第 $i$ ($1 \leq i \leq n$) 行包含一个非负整数，表示第 $i$ 次操作后的优美的 DFS 序的数量对 $1,000,000,007$ 取模后的结果。

样例 1 解释

该样例即【题目描述】中所示的例子。

• 第一次操作后，叶子结点 $4$ 和 $6$ 上标有数字 $1$，叶子结点 $5$ 和 $7$ 上没有数字，因此按任意 DFS 序拼成的序列均为 $[1, 1]$，即所有的 $2^3 = 8$ 个 DFS 序都是优美的。
• 第二次操作后，叶子结点 $4 \sim 7$ 上分别标有数字 $1, 2, 1, 2$，因此共有 $4$ 个优美的 DFS 序，分别为 $[1, 4, 2, 3, 6, 5, 7], [1, 4, 2, 7, 3, 5, 6], [1, 2, 3, 6, 5, 7, 4], [1, 2, 7, 3, 5, 6, 4]$。

样例 3

该样例满足测试点 $6 \sim 10$ 的约束条件。

样例 4

该样例满足测试点 $11, 12$ 的约束条件。

样例 5

该样例满足测试点 $17 \sim 20$ 的约束条件。

样例 6

该样例满足测试点 $24, 25$ 的约束条件。

数据范围

对于所有测试数据，保证：

• $1 \leq n \leq 2 \times 10^5$；
• 对于所有 $1 \leq i \leq 2n - 1$，均有 $i < l_i, r_i \leq 4n - 1$，且所有的 $l_i, r_i$ 互不相同；
• 对于所有 $1 \leq i \leq n$，均有 $2n \leq a_i, b_i \leq 4n - 1$，且所有的 $a_i, b_i$ 互不相同；
• 在每次操作后，存在至少一个优美的 DFS 序。

测试点编号	$n \leq$	特殊性质
$1, 2$	$10$	无
$3 \sim 5$	$10^2$	A
$6 \sim 10$	$10^2$	无
$11, 12$	$10^3$	A
$13, 14$	$10^3$	无
$15, 16$	$5 \times 10^4$	AB
$17 \sim 20$	$5 \times 10^4$	B
$21, 22$	$5 \times 10^4$	无
$23$	$2 \times 10^5$	A
$24, 25$	$2 \times 10^5$	无

特殊性质 A：保证每次操作选择的两个叶子结点位于结点 1 的不同子树内。

特殊性质 B：保证存在非负整数 $m$ 满足 $n = 2^m$，且对于所有 $1 \leq i \leq 2n - 1$，均有 $l_i = 2i, r_i = 2i + 1$。