A21616.时空穿梭

小X驾驶着他的飞船准备穿梭过一个 $n$ 维空间，这个空间里每个点的坐标可以用 $n$ 个实数来表示，即 $(x_1, x_2, ... , x_n)$ 。

为了穿过这个空间，小 X 需要在这个空间中选取 $c$ $(c \geq 2)$ 个点作为飞船停留的地方，而这些点需要满足以下三个条件：

$1$. 每个点的每一维坐标均为正整数，且第 $i$ 维坐标不超过 $m_i$ 。

$2$. 第 $i + 1$ $(1 \leq i < c)$ 个点的第 $j$ $(1 \leq j \leq n)$ 维坐标必须严格大于第 $i$ 个点的第 $j$ 维坐标。

$3$. 存在一条直线经过所选的所有点。在这个 $n$ 维空间里，一条直线可以用 $2n$个实数 $p_1$, $p_2$, … , $p_n$, $v_1$, $v_2$, … , $v_n$ 表示。 直线经过点 $(x_1, x_2, ... , x_n)$ ，当且仅当存在实数 $t$，使得对 $i = 1$ … $n$ 均满足 $x_i$ = $p_i + tv_i$。

小 X 还没有确定他的最终方案，请你帮他计算一下一共有多少种不同的方案满足他的要求。由于答案可能会很大，你只需要输出答案 mod $10 007$ 后的值。

输入文件 space.in 的第一行包含一个正整数 $T$ ，表示有 $T$ 组数据需要求解。

每组数据包含两行，第一行包含两个正整数 $n$, $c$ $(c \geq 2)$ ，分别表示空间的维数和需要选择的暂停点个数。

第二行包含 $n$ 个正整数，依次表示 $m_1$, $m_2$, … , $m_n$。

输出文件 space.out 包含 $T$ 行，每行包含一个非负整数，依次对应每组数据

的答案。

【样例$1$说明】

样例数据第一组共有两种可行方案：一种是选择 $(1,1)$ , $(2,2)$ , $(3,3)$ ，另一种是选择 $(1,2)$ , $(2,3)$ , $(3,4)$ 。

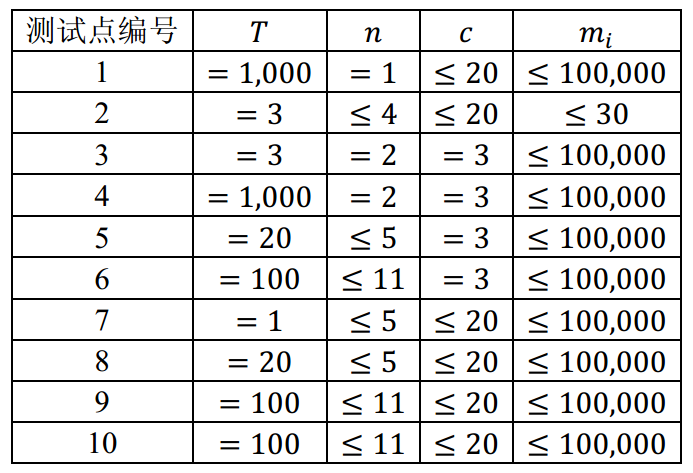
【数据规模】