CF1770E.Koxia and Tree

Imi has an undirected tree with $n$ vertices where edges are numbered from $1$ to $n-1$ . The $i$ -th edge connects vertices $u_i$ and $v_i$ . There are also $k$ butterflies on the tree. Initially, the $i$ -th butterfly is on vertex $a_i$ . All values of $a$ are pairwise distinct.

Koxia plays a game as follows:

• For $i = 1, 2, \dots, n - 1$ , Koxia set the direction of the $i$ -th edge as $u_i \rightarrow v_i$ or $v_i \rightarrow u_i$ with equal probability.
• For $i = 1, 2, \dots, n - 1$ , if a butterfly is on the initial vertex of $i$ -th edge and there is no butterfly on the terminal vertex, then this butterfly flies to the terminal vertex. Note that operations are sequentially in order of $1, 2, \dots, n - 1$ instead of simultaneously.
• Koxia chooses two butterflies from the $k$ butterflies with equal probability from all possible $\frac{k(k-1)}{2}$ ways to select two butterflies, then she takes the distance $^\dagger$ between the two chosen vertices as her score.

Now, Koxia wants you to find the expected value of her score, modulo $998\,244\,353^\ddagger$ .

$^\dagger$ The distance between two vertices on a tree is the number of edges on the (unique) simple path between them.

$^\ddagger$ Formally, let $M = 998\,244\,353$ . It can be shown that the answer can be expressed as an irreducible fraction $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \not \equiv 0 \pmod{M}$ . Output the integer equal to $p \cdot q^{-1} \bmod M$ . In other words, output such an integer $x$ that $0 \le x < M$ and $x \cdot q \equiv p \pmod{M}$ .

The first line contains two integers $n$ , $k$ ( $2 \leq k \leq n \leq 3 \cdot {10}^5$ ) — the size of the tree and the number of butterflies.

The second line contains $k$ integers $a_1, a_2, \dots, a_k$ ( $1 \leq a_i \leq n$ ) — the initial position of butterflies. It's guaranteed that all positions are distinct.

The $i$ -th line in following $n − 1$ lines contains two integers $u_i$ , $v_i$ ( $1 \leq u_i, v_i \leq n$ , $u_i \neq v_i$ ) — the vertices the $i$ -th edge connects.

It is guaranteed that the given edges form a tree.

Output a single integer — the expected value of Koxia's score, modulo $998\,244\,353$ .

In the first test case, the tree is shown below. Vertices containing butterflies are noted as bold.

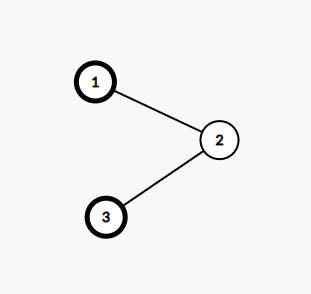There are only $2$ butterflies so the choice of butterflies is fixed. Let's consider the following $4$ cases:

• Edges are $1 \rightarrow 2$ and $2 \rightarrow 3$ : butterfly on vertex $1$ moves to vertex $2$ , but butterfly on vertex $3$ doesn't move. The distance between vertices $2$ and $3$ is $1$ .
• Edges are $1 \rightarrow 2$ and $3 \rightarrow 2$ : butterfly on vertex $1$ moves to vertex $2$ , but butterfly on vertex $3$ can't move to vertex $2$ because it's occupied. The distance between vertices $2$ and $3$ is $1$ .
• Edges are $2 \rightarrow 1$ and $2 \rightarrow 3$ : butterflies on both vertex $1$ and vertex $3$ don't move. The distance between vertices $1$ and $3$ is $2$ .
• Edges are $2 \rightarrow 1$ and $3 \rightarrow 2$ : butterfly on vertex $1$ doesn't move, but butterfly on vertex $3$ move to vertex $2$ . The distance between vertices $1$ and $2$ is $1$ .

Therefore, the expected value of Koxia's score is $\frac {1+1+2+1} {4} = \frac {5} {4}$ , which is $748\,683\,266$ after modulo $998\,244\,353$ .

In the second test case, the tree is shown below. Vertices containing butterflies are noted as bold. The expected value of Koxia's score is $\frac {11} {6}$ , which is $831\,870\,296$ after modulo $998\,244\,353$ .