CF1775D.Friendly Spiders

Mars is home to an unusual species of spiders — Binary spiders.

Right now, Martian scientists are observing a colony of $n$ spiders, the $i$ -th of which has $a_i$ legs.

Some of the spiders are friends with each other. Namely, the $i$ -th and $j$ -th spiders are friends if $\gcd(a_i, a_j) \ne 1$ , i. e., there is some integer $k \ge 2$ such that $a_i$ and $a_j$ are simultaneously divided by $k$ without a remainder. Here $\gcd(x, y)$ denotes the greatest common divisor (GCD) of integers $x$ and $y$ .

Scientists have discovered that spiders can send messages. If two spiders are friends, then they can transmit a message directly in one second. Otherwise, the spider must pass the message to his friend, who in turn must pass the message to his friend, and so on until the message reaches the recipient.

Let's look at an example.

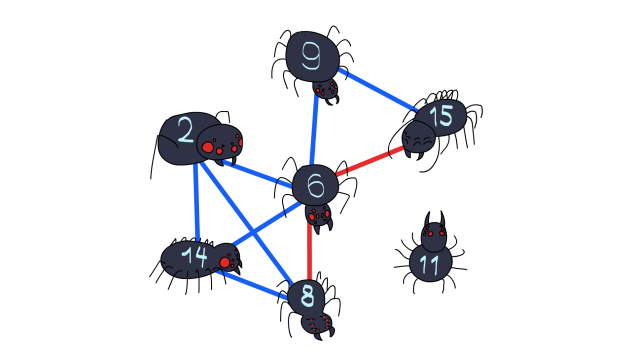
Suppose a spider with eight legs wants to send a message to a spider with $15$ legs. He can't do it directly, because $\gcd(8, 15) = 1$ . But he can send a message through the spider with six legs because $\gcd(8, 6) = 2$ and $\gcd(6, 15) = 3$ . Thus, the message will arrive in two seconds.

Right now, scientists are observing how the $s$ -th spider wants to send a message to the $t$ -th spider. The researchers have a hypothesis that spiders always transmit messages optimally. For this reason, scientists would need a program that could calculate the minimum time to send a message and also deduce one of the optimal routes.

The first line of input contains an integer $n$ ( $2 \le n \le 3\cdot10^5$ ) — the number of spiders in the colony.

The second line of input contains $n$ integers $a_1, a_2, \ldots, a_n$ ( $1 \le a_i \le 3\cdot10^5$ ) — the number of legs the spiders have.

The third line of input contains two integers $s$ and $t$ ( $1 \le s, t \le n$ ) —the spiders between which the message must be sent.

If it is impossible to transmit a message between the given pair of spiders, print $-1$ .

Otherwise, in the first line of the output print the integer $t$ ( $t \ge 1$ ) — the number of spiders that participate in the message transmission (i. e. the minimum time of message delivery in seconds plus one). In the second line, print $t$ different integers $b_1, b_2, \ldots, b_t$ ( $1 \le b_i \le n$ ) — the ids of the spiders through which the message should follow, in order from sender to receiver.

If there are several optimal routes for the message, output any of them.

The first example is shown above. It shows that the message from the $5$ -th spider (with eight legs) to the $6$ -th spider (with $15$ legs) is optimal to pass through the $4$ -th spider (with six legs).

In the second example, the spider number $7$ (with $11$ legs) is not friends with anyone, so it is impossible to send him a message.