CF1777D.Score of a Tree

You are given a tree of $n$ nodes, rooted at $1$ . Every node has a value of either $0$ or $1$ at time $t=0$ .

At any integer time $t>0$ , the value of a node becomes the bitwise XOR of the values of its children at time $t - 1$ ; the values of leaves become $0$ since they don't have any children.

Let $S(t)$ denote the sum of values of all nodes at time $t$ .

Let $F(A)$ denote the sum of $S(t)$ across all values of $t$ such that $0 \le t \le 10^{100}$ , where $A$ is the initial assignment of $0$ s and $1$ s in the tree.

The task is to find the sum of $F(A)$ for all $2^n$ initial configurations of $0$ s and $1$ s in the tree. Print the sum modulo $10^9+7$ .

Each test contains multiple test cases. The first line contains the number of test cases $t$ ( $1 \le t \le 10^5$ ). The description of the test cases follows.

The first line of each test case contains $n$ ( $1 \le n \le 2 \cdot 10^5$ ) — the number of nodes in the tree.

The next $n-1$ lines of each test case contain two integers each — $u$ , $v$ indicating an edge between $u$ and $v$ ( $1 \le u, v \le n$ ).

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$ .

Output the sum modulo $10^9+7$ for each test case.

Let us find $F(A)$ for the configuration $A = [0,1,0,0,1,1]$ ( $A[i]$ denotes the value of node $i$ ). Initially (at $t = 0$ ) our tree is as shown in the picture below. In each node, two values are shown: the number and the value of this node. $S(0)$ for this configuration is $3$ .

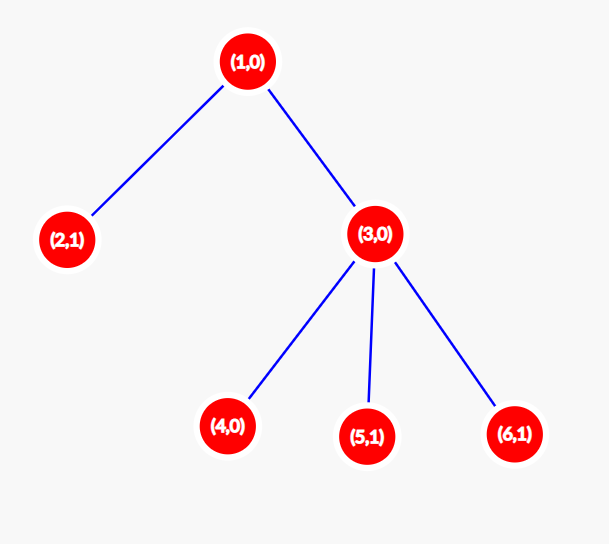At $t = 1$ the configuration changes to $[1,0,0,0,0,0]$ . The tree looks as shown below. $S(1) = 1$ .

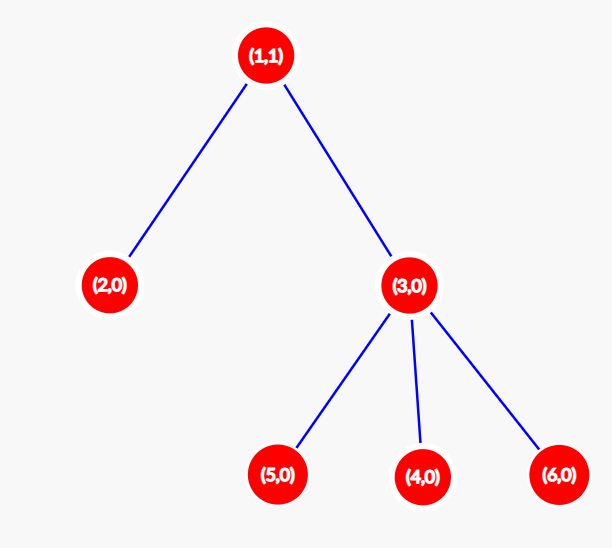At $t = 2$ the configuration changes to $[0,0,0,0,0,0]$ . The tree looks as shown below. $S(2) = 0$ .

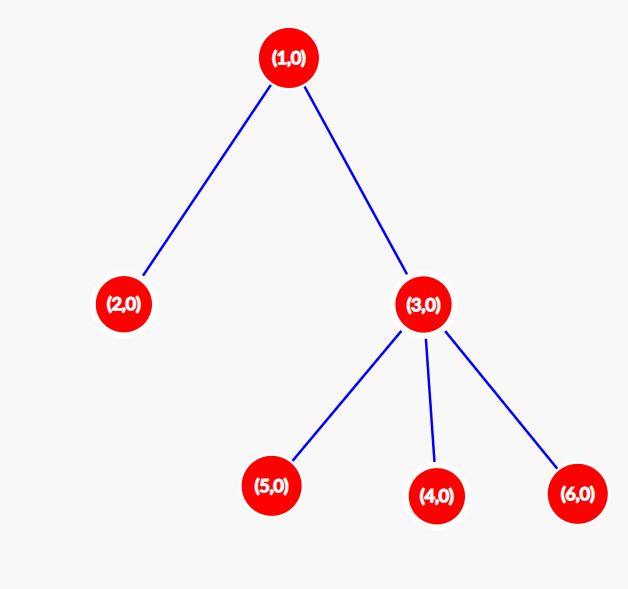For all $t>2$ , the graph remains unchanged, so $S(t)=0$ for all $t > 2$ . So, for the initial configuration $A = [0,1,0,0,1,1]$ , the value of $F(A) = 3 + 1 = 4$ .

Doing this process for all possible $2^{6}$ configurations yields us an answer of $\textbf{288}$ .