CF1764C.Doremy's City Construction

Doremy's new city is under construction! The city can be regarded as a simple undirected graph with $n$ vertices. The $i$ -th vertex has altitude $a_i$ . Now Doremy is deciding which pairs of vertices should be connected with edges.

Due to economic reasons, there should be no self-loops or multiple edges in the graph.

Due to safety reasons, there should not be pairwise distinct vertices $u$ , $v$ , and $w$ such that $a_u \leq a_v \leq a_w$ and the edges $(u,v)$ and $(v,w)$ exist.

Under these constraints, Doremy would like to know the maximum possible number of edges in the graph. Can you help her?

Note that the constructed graph is allowed to be disconnected.

The input consists of multiple test cases. The first line contains a single integer $t$ ( $1\le t\le 10^4$ ) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $2 \le n \le 2\cdot 10^5$ ) — the number of vertices.

The second line of each test case contains $n$ integers $a_1, a_2, \dots, a_n$ ( $1\le a_i\le 10^6$ ) — the altitudes of each vertex.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$ .

For each test case, output the maximum possible number of edges in the graph.

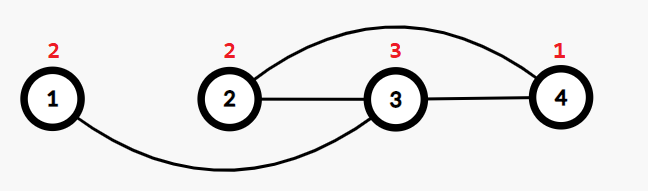
In the first test case, there can only be at most $3$ edges in the graph. A possible construction is to connect $(1,3)$ , $(2,3)$ , $(3,4)$ . In the picture below the red number above node $i$ is $a_i$ .

The following list shows all such $u$ , $v$ , $w$ that the edges $(u,v)$ and $(v,w)$ exist.

• $u=1$ , $v=3$ , $w=2$ ;
• $u=1$ , $v=3$ , $w=4$ ;
• $u=2$ , $v=3$ , $w=1$ ;
• $u=2$ , $v=3$ , $w=4$ ;
• $u=4$ , $v=3$ , $w=1$ ;
• $u=4$ , $v=3$ , $w=2$ .

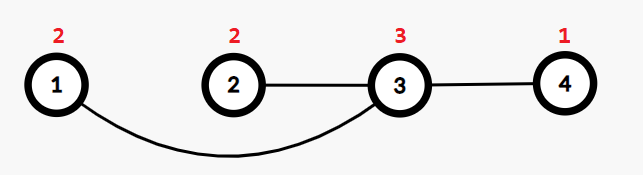
Another possible construction is to connect $(1,4)$ , $(2,4)$ , $(3,4)$ .

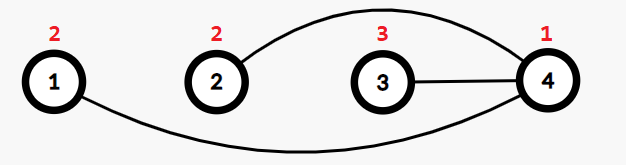
An unacceptable construction is to connect $(1,3)$ , $(2,3)$ , $(2,4)$ , $(3,4)$ . Because when $u=4$ , $v=2$ , $w=3$ , $a_u\le a_v \le a_w$ holds, and the respective edges exist.