CF1764F.Doremy's Experimental Tree

Doremy has an edge-weighted tree with $n$ vertices whose weights are integers between $1$ and $10^9$ . She does $\frac{n(n+1)}{2}$ experiments on it.

In each experiment, Doremy chooses vertices $i$ and $j$ such that $j \leq i$ and connects them directly with an edge with weight $1$ . Then, there is exactly one cycle (or self-loop when $i=j$ ) in the graph. Doremy defines $f(i,j)$ as the sum of lengths of shortest paths from every vertex to the cycle.

Formally, let $\mathrm{dis}_{i,j}(x,y)$ be the length of the shortest path between vertex $x$ and $y$ when the edge $(i,j)$ of weight $1$ is added, and $S_{i,j}$ be the set of vertices that are on the cycle when edge $(i,j)$ is added. Then,

$$f(i,j)=\sum_{x=1}^{n}\left(\min_{y\in S_{i,j}}\mathrm{dis}_{i,j}(x,y)\right).$$

Doremy writes down all values of $f(i,j)$ such that $1 \leq j \leq i \leq n$ , then goes to sleep. However, after waking up, she finds that the tree has gone missing. Fortunately, the values of $f(i,j)$ are still in her notebook, and she knows which $i$ and $j$ they belong to. Given the values of $f(i,j)$, can you help her restore the tree?

It is guaranteed that at least one suitable tree exists.

The first line of input contains a single integer $n$ ($2 \le n \le 2000$) — the number of vertices in the tree.

The following $n$ lines contain a lower-triangular matrix with $i$ integers on the $i$ -th line; the $j$ -th integer on the $i$ -th line is $f(i,j)$ ( $0 \le f(i,j) \le 2\cdot 10^{15}$ ).

It is guaranteed that there exists a tree whose weights are integers between $1$ and $10^9$ such that the values of $f(i,j)$ of the tree match those given in the input.

Print $n-1$ lines describing the tree. In the $i$ -th line of the output, output three integers $u_i$ , $v_i$ , $w_i$ ( $1 \le u_i,v_i \le n$ , $1 \le w_i \le 10^9$ ), representing an edge $(u_i,v_i)$ whose weight is $w_i$ .

If there are multiple answers, you may output any.

All edges must form a tree and all values of $f(i,j)$ must match those given in the input.

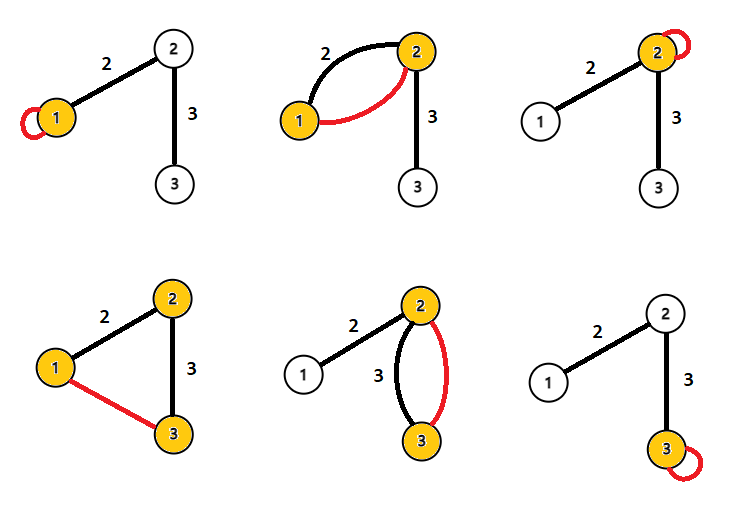
In the first test case, the picture below, from left to right, from top to bottom, shows the graph when pairs $(1,1)$ , $(1,2)$ , $(1,3)$ , $(2,2)$ , $(2,3)$ , $(3,3)$ are connected with an edge, respectively. The nodes colored yellow are on the cycle.