CF1735D.Meta-set

You like the card board game "Set". Each card contains $k$ features, each of which is equal to a value from the set $\{0, 1, 2\}$ . The deck contains all possible variants of cards, that is, there are $3^k$ different cards in total.

A feature for three cards is called good if it is the same for these cards or pairwise distinct. Three cards are called a set if all $k$ features are good for them.

For example, the cards $(0, 0, 0)$ , $(0, 2, 1)$ , and $(0, 1, 2)$ form a set, but the cards $(0, 2, 2)$ , $(2, 1, 2)$ , and $(1, 2, 0)$ do not, as, for example, the last feature is not good.

A group of five cards is called a meta-set, if there is strictly more than one set among them. How many meta-sets there are among given $n$ distinct cards?

The first line of the input contains two integers $n$ and $k$ ( $1 \le n \le 10^3$ , $1 \le k \le 20$ ) — the number of cards on a table and the number of card features. The description of the cards follows in the next $n$ lines.

Each line describing a card contains $k$ integers $c_{i, 1}, c_{i, 2}, \ldots, c_{i, k}$ ( $0 \le c_{i, j} \le 2$ ) — card features. It is guaranteed that all cards are distinct.

Output one integer — the number of meta-sets.

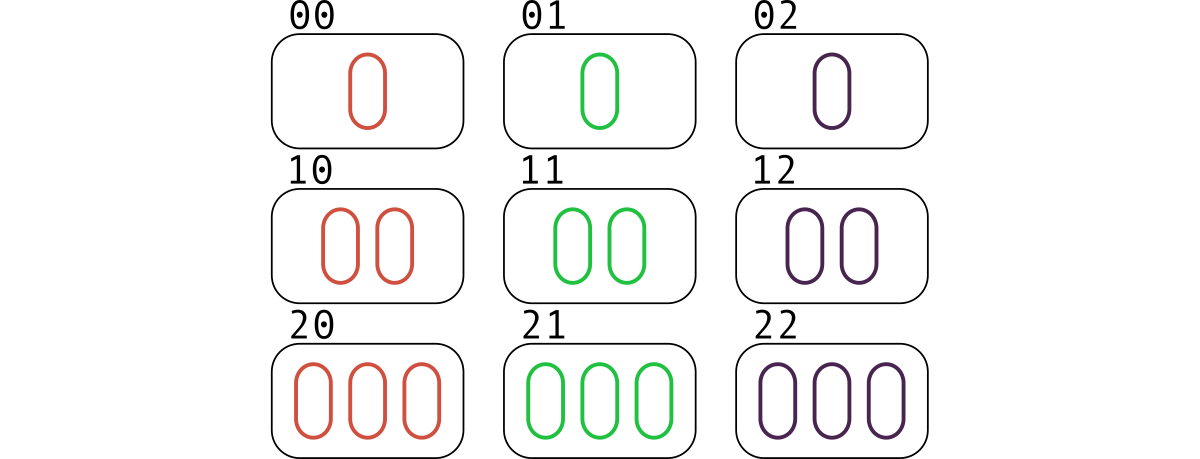
Let's draw the cards indicating the first four features. The first feature will indicate the number of objects on a card: $1$ , $2$ , $3$ . The second one is the color: red, green, purple. The third is the shape: oval, diamond, squiggle. The fourth is filling: open, striped, solid.

You can see the first three tests below. For the first two tests, the meta-sets are highlighted.

In the first test, the only meta-set is the five cards $(0000,\ 0001,\ 0002,\ 0010,\ 0020)$ . The sets in it are the triples $(0000,\ 0001,\ 0002)$ and $(0000,\ 0010,\ 0020)$ . Also, a set is the triple $(0100,\ 1000,\ 2200)$ which does not belong to any meta-set.

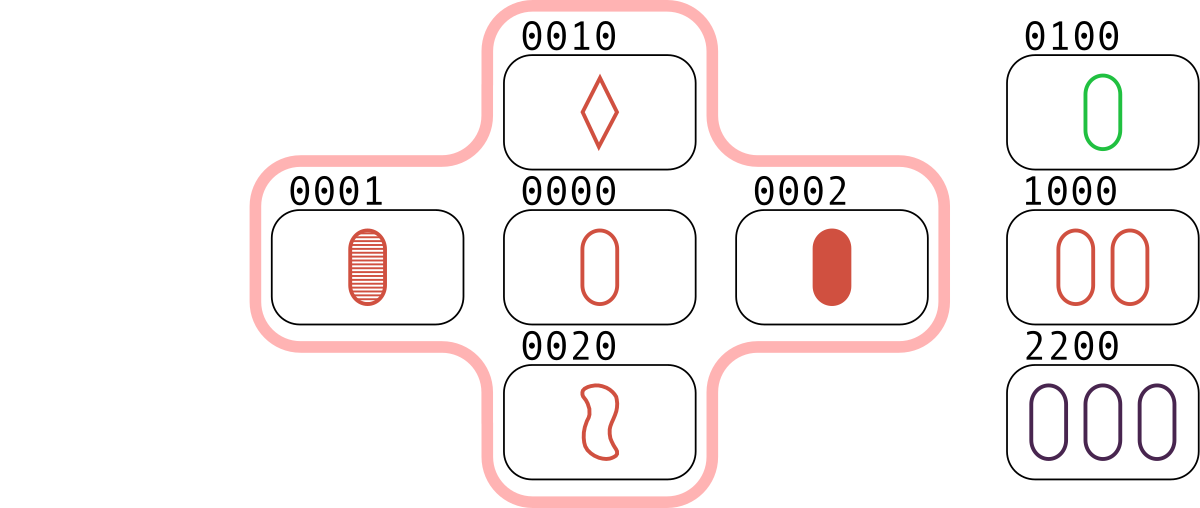In the second test, the following groups of five cards are meta-sets: $(0000,\ 0001,\ 0002,\ 0010,\ 0020)$ , $(0000,\ 0001,\ 0002,\ 0100,\ 0200)$ , $(0000,\ 0010,\ 0020,\ 0100,\ 0200)$ .

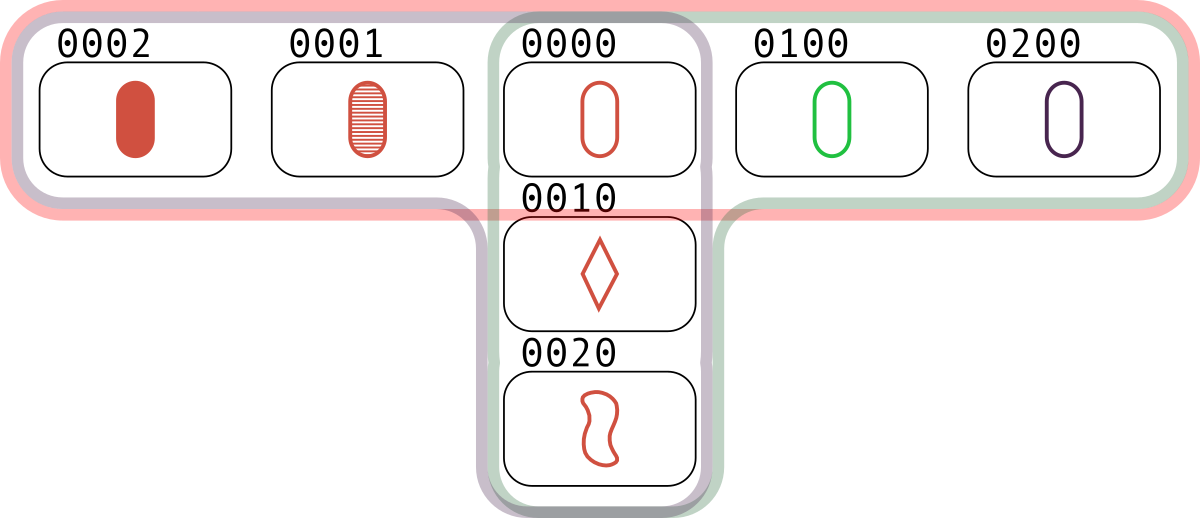In there third test, there are $54$ meta-sets.