CF1740E.Hanging Hearts

Pak Chanek has $n$ blank heart-shaped cards. Card $1$ is attached directly to the wall while each of the other cards is hanging onto exactly one other card by a piece of string. Specifically, card $i$ ( $i > 1$ ) is hanging onto card $p_i$ ( $p_i < i$ ).

In the very beginning, Pak Chanek must write one integer number on each card. He does this by choosing any permutation $a$ of $[1, 2, \dots, n]$ . Then, the number written on card $i$ is $a_i$ .

After that, Pak Chanek must do the following operation $n$ times while maintaining a sequence $s$ (which is initially empty):

1. Choose a card $x$ such that no other cards are hanging onto it.
2. Append the number written on card $x$ to the end of $s$ .
3. If $x \neq 1$ and the number on card $p_x$ is larger than the number on card $x$ , replace the number on card $p_x$ with the number on card $x$ .
4. Remove card $x$ .

After that, Pak Chanek will have a sequence $s$ with $n$ elements. What is the maximum length of the longest non-decreasing subsequence $^\dagger$ of $s$ at the end if Pak Chanek does all the steps optimally?

$^\dagger$ A sequence $b$ is a subsequence of a sequence $c$ if $b$ can be obtained from $c$ by deletion of several (possibly, zero or all) elements. For example, $[3,1]$ is a subsequence of $[3,2,1]$ , $[4,3,1]$ and $[3,1]$ , but not $[1,3,3,7]$ and $[3,10,4]$ .

The first line contains a single integer $n$ ( $2 \le n \le 10^5$ ) — the number of heart-shaped cards.

The second line contains $n - 1$ integers $p_2, p_3, \dots, p_n$ ( $1 \le p_i < i$ ) describing which card that each card hangs onto.

Print a single integer — the maximum length of the longest non-decreasing subsequence of $s$ at the end if Pak Chanek does all the steps optimally.

The following is the structure of the cards in the first example.

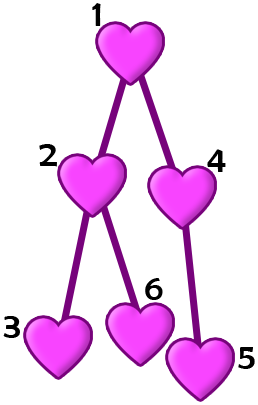
Pak Chanek can choose the permutation $a = [1, 5, 4, 3, 2, 6]$ .

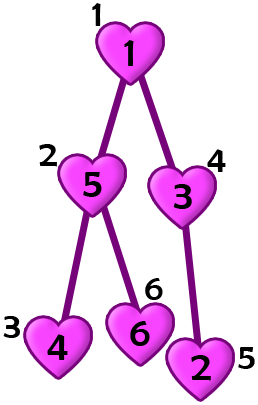
Let $w_i$ be the number written on card $i$ . Initially, $w_i = a_i$ . Pak Chanek can do the following operations in order:

1. Select card $5$ . Append $w_5 = 2$ to the end of $s$ . As $w_4 > w_5$ , the value of $w_4$ becomes $2$ . Remove card $5$ . After this operation, $s = [2]$ .
2. Select card $6$ . Append $w_6 = 6$ to the end of $s$ . As $w_2 \leq w_6$ , the value of $w_2$ is left unchanged. Remove card $6$ . After this operation, $s = [2, 6]$ .
3. Select card $4$ . Append $w_4 = 2$ to the end of $s$ . As $w_1 \leq w_4$ , the value of $w_1$ is left unchanged. Remove card $4$ . After this operation, $s = [2, 6, 2]$ .
4. Select card $3$ . Append $w_3 = 4$ to the end of $s$ . As $w_2 > w_3$ , the value of $w_2$ becomes $4$ . Remove card $3$ . After this operation, $s = [2, 6, 2, 4]$ .
5. Select card $2$ . Append $w_2 = 4$ to the end of $s$ . As $w_1 \leq w_2$ , the value of $w_1$ is left unchanged. Remove card $2$ . After this operation, $s = [2, 6, 2, 4, 4]$ .
6. Select card $1$ . Append $w_1 = 1$ to the end of $s$ . Remove card $1$ . After this operation, $s = [2, 6, 2, 4, 4, 1]$ .

One of the longest non-decreasing subsequences of $s = [2, 6, 2, 4, 4, 1]$ is $[2, 2, 4, 4]$ . Thus, the length of the longest non-decreasing subsequence of $s$ is $4$ . It can be proven that this is indeed the maximum possible length.