CF1717D.Madoka and The Corruption Scheme

Madoka decided to entrust the organization of a major computer game tournament "OSU"!

In this tournament, matches are held according to the "Olympic system". In other words, there are $2^n$ participants in the tournament, numbered with integers from $1$ to $2^n$ . There are $n$ rounds in total in the tournament. In the $i$ -th round there are $2^{n - i}$ matches between two players (one of whom is right, the other is left), after which the winners go further along the tournament grid, and the losing participants are eliminated from the tournament. Herewith, the relative order in the next round does not change. And the winner of the tournament — is the last remaining participant.

But the smaller the participant's number, the more he will pay Madoka if he wins, so Madoka wants the participant with the lowest number to win. To do this, she can arrange the participants in the first round as she likes, and also determine for each match who will win — the participant on the left or right.

But Madoka knows that tournament sponsors can change the winner in matches no more than $k$ times. (That is, if the participant on the left won before the change, then the participant on the right will win after the change, and if the participant on the right won, then the participant on the left will win after the change).

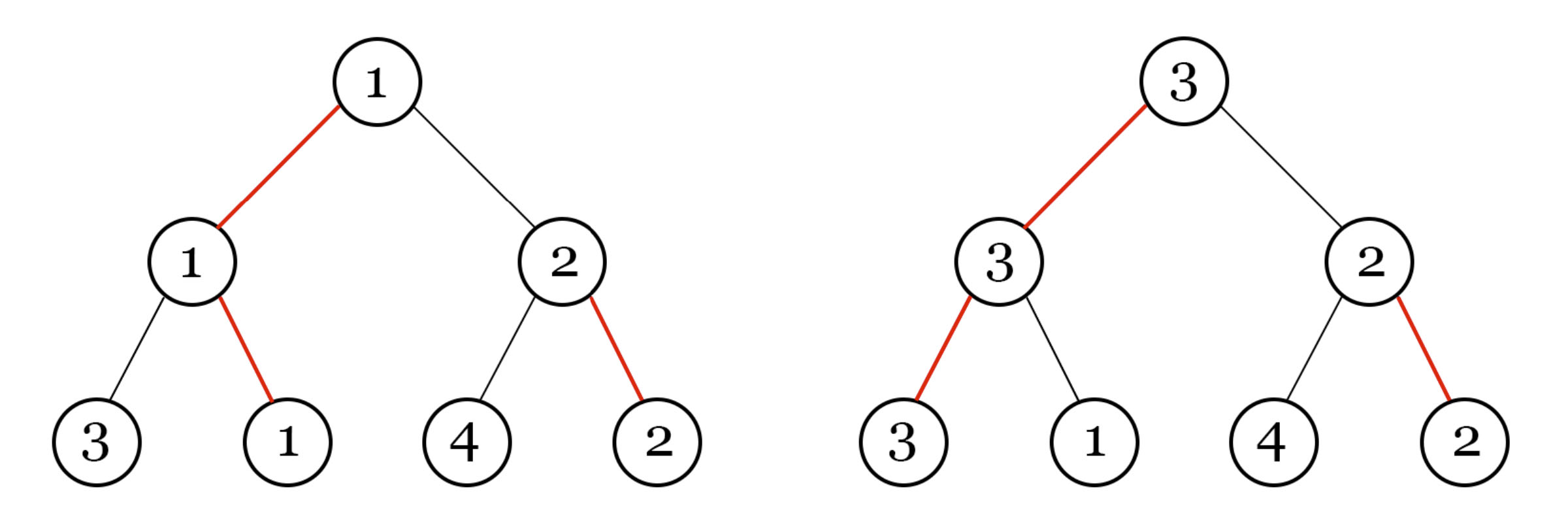So, the first image shows the tournament grid that Madoka made, where the red lines denote who should win the match. And the second one shows the tournament grid, after one change in the outcome of the match by sponsors (a match between $1$ and $3$ players).Print the minimum possible number of the winner in the tournament, which Madoka can get regardless of changes in sponsors. But since the answer can be very large, output it modulo $10^9 + 7$ . Note that we need to minimize the answer, and only then take it modulo.

The first and the only line contains two integers $n$ and $k$ ( $1 \le n \le 10^5, 1 \le k \le \min(2^n - 1, 10^9)$ ) — the number of rounds in the tournament and the number of outcomes that sponsors can change.

Print exactly one integer — the minimum number of the winner modulo $10^9 + 7$

In the first example, there is only one match between players $1$ and $2$ , so the sponsors can always make player $2$ wins.

The tournament grid from the second example is shown in the picture in the statement.