CF1712D.Empty Graph

— Do you have a wish?

— I want people to stop gifting each other arrays.

O_o and Another Young Boy

An array of $n$ positive integers $a_1,a_2,\ldots,a_n$ fell down on you from the skies, along with a positive integer $k \le n$ .

You can apply the following operation at most $k$ times:

• Choose an index $1 \le i \le n$ and an integer $1 \le x \le 10^9$ . Then do $a_i := x$ (assign $x$ to $a_i$ ).

Then build a complete undirected weighted graph with $n$ vertices numbered with integers from $1$ to $n$ , where edge $(l, r)$ ( $1 \le l < r \le n$ ) has weight $\min(a_{l},a_{l+1},\ldots,a_{r})$ .

You have to find the maximum possible diameter of the resulting graph after performing at most $k$ operations.

The diameter of a graph is equal to $\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$ , where $\operatorname{d}(u, v)$ is the length of the shortest path between vertex $u$ and vertex $v$ .

Each test contains multiple test cases. The first line contains the number of test cases $t$ ( $1 \le t \le 10^4$ ). Description of the test cases follows.

The first line of each test case contains two integers $n$ and $k$ ( $2 \le n \le 10^5$ , $1 \le k \le n$ ).

The second line of each test case contains $n$ positive integers $a_1,a_2,\ldots,a_n$ ( $1 \le a_i \le 10^9$ ).

It is guaranteed that the sum of $n$ over all test cases does not exceed $10^5$ .

For each test case print one integer — the maximum possible diameter of the graph after performing at most $k$ operations.

In the first test case, one of the optimal arrays is $[2,4,5]$ .

The graph built on this array:

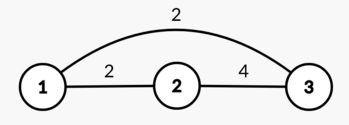$\operatorname{d}(1, 2) = \operatorname{d}(1, 3) = 2$ and $\operatorname{d}(2, 3) = 4$ , so the diameter is equal to $\max(2,2,4) = 4$ .