CF1690A.Print a Pedestal (Codeforces logo?)

Given the integer $n$ — the number of available blocks. You must use all blocks to build a pedestal.

The pedestal consists of $3$ platforms for $2$ -nd, $1$ -st and $3$ -rd places respectively. The platform for the $1$ -st place must be strictly higher than for the $2$ -nd place, and the platform for the $2$ -nd place must be strictly higher than for the $3$ -rd place. Also, the height of each platform must be greater than zero (that is, each platform must contain at least one block).

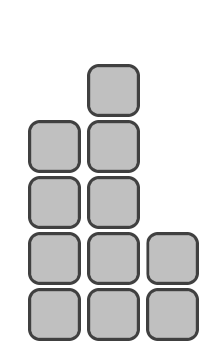Example pedestal of $n=11$ blocks: second place height equals $4$ blocks, first place height equals $5$ blocks, third place height equals $2$ blocks.Among all possible pedestals of $n$ blocks, deduce one such that the platform height for the $1$ -st place minimum as possible. If there are several of them, output any of them.

The first line of input data contains an integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases.

Each test case contains a single integer $n$ ( $6 \le n \le 10^5$ ) — the total number of blocks for the pedestal. All $n$ blocks must be used.

It is guaranteed that the sum of $n$ values over all test cases does not exceed $10^6$ .

For each test case, output $3$ numbers $h_2, h_1, h_3$ — the platform heights for $2$ -nd, $1$ -st and $3$ -rd places on a pedestal consisting of $n$ blocks ( $h_1+h_2+h_3=n$ , $0 < h_3 < h_2 < h_1$ ).

Among all possible pedestals, output the one for which the value of $h_1$ minimal. If there are several of them, output any of them.

In the first test case we can not get the height of the platform for the first place less than $5$ , because if the height of the platform for the first place is not more than $4$ , then we can use at most $4 + 3 + 2 = 9$ blocks. And we should use $11 = 4 + 5 + 2$ blocks. Therefore, the answer 4 5 2 fits.

In the second set, the only suitable answer is: 2 3 1.