CF1691F.K-Set Tree

You are given a tree $G$ with $n$ vertices and an integer $k$ . The vertices of the tree are numbered from $1$ to $n$ .

For a vertex $r$ and a subset $S$ of vertices of $G$ , such that $|S| = k$ , we define $f(r, S)$ as the size of the smallest rooted subtree containing all vertices in $S$ when the tree is rooted at $r$ . A set of vertices $T$ is called a rooted subtree, if all the vertices in $T$ are connected, and for each vertex in $T$ , all its descendants belong to $T$ .

You need to calculate the sum of $f(r, S)$ over all possible distinct combinations of vertices $r$ and subsets $S$ , where $|S| = k$ . Formally, compute the following: $$$$\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S), $$ where $V$ is the set of vertices in $G$ .

Output the answer modulo $10^9 + 7$$$.

The first line contains two integers $n$ and $k$ ( $3 \le n \le 2 \cdot 10^5$ , $1 \le k \le n$ ).

Each of the following $n - 1$ lines contains two integers $x$ and $y$ ( $1 \le x, y \le n$ ), denoting an edge between vertex $x$ and $y$ .

It is guaranteed that the given edges form a tree.

Print the answer modulo $10^9 + 7$ .

The tree in the second example is given below:

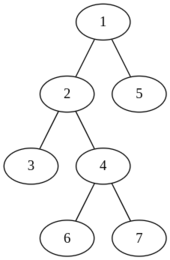We have $21$ subsets of size $2$ in the given tree. Hence, $$$$S \in \left{{1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {1, 7}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {2, 7}, {3, 4}, {3, 5}, {3, 6}, {3, 7}, {4, 5}, {4, 6}, {4, 7}, {5, 6}, {5, 7}, {6, 7} \right}. $$ And since we have $7$ vertices, $1 \\le r \\le 7$ . We need to find the sum of $f(r, S)$ over all possible pairs of $r$ and $S$ .

Below we have listed the value of $f(r, S)$ for some combinations of $r$ and $S$ .

• $r = 1$ , $S = \\{3, 7\\}$ . The value of $f(r, S)$ is $5$ and the corresponding subtree is $\\{2, 3, 4, 6, 7\\}$ .
• $r = 1$ , $S = \\{5, 4\\}$ . The value of $f(r, S)$ is $7$ and the corresponding subtree is $\\{1, 2, 3, 4, 5, 6, 7\\}$ .
• $r = 1$ , $S = \\{4, 6\\}$ . The value of $f(r, S)$ is $3$ and the corresponding subtree is $\\{4, 6, 7\\}$$$.