CF1665C.Tree Infection

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. The parent of a vertex $v$ (different from root) is the previous to $v$ vertex on the shortest path from the root to the vertex $v$ . Children of the vertex $v$ are all vertices for which $v$ is the parent.

You are given a rooted tree with $n$ vertices. The vertex $1$ is the root. Initially, all vertices are healthy.

Each second you do two operations, the spreading operation and, after that, the injection operation:

Spreading: for each vertex $v$ , if at least one child of $v$ is infected, you can spread the disease by infecting at most one other child of $v$ of your choice.
Injection: you can choose any healthy vertex and infect it.

This process repeats each second until the whole tree is infected. You need to find the minimal number of seconds needed to infect the whole tree.

输入格式

The input consists of multiple test cases. The first line contains a single integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases. Description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $2 \le n \le 2 \cdot 10^5$ ) — the number of the vertices in the given tree.

The second line of each test case contains $n - 1$ integers $p_2, p_3, \ldots, p_n$ ( $1 \le p_i \le n$ ), where $p_i$ is the ancestor of the $i$ -th vertex in the tree.

It is guaranteed that the given graph is a tree.

It is guaranteed that the sum of $n$ over all test cases doesn't exceed $2 \cdot 10^5$ .

输出格式

For each test case you should output a single integer — the minimal number of seconds needed to infect the whole tree.

输入输出样例

输入#1

5
7
1 1 1 2 2 4
5
5 5 1 4
2
1
3
3 1
6
1 1 1 1 1

输出#1

说明/提示

The image depicts the tree from the first test case during each second.

A vertex is black if it is not infected. A vertex is blue if it is infected by injection during the previous second. A vertex is green if it is infected by spreading during the previous second. A vertex is red if it is infected earlier than the previous second.

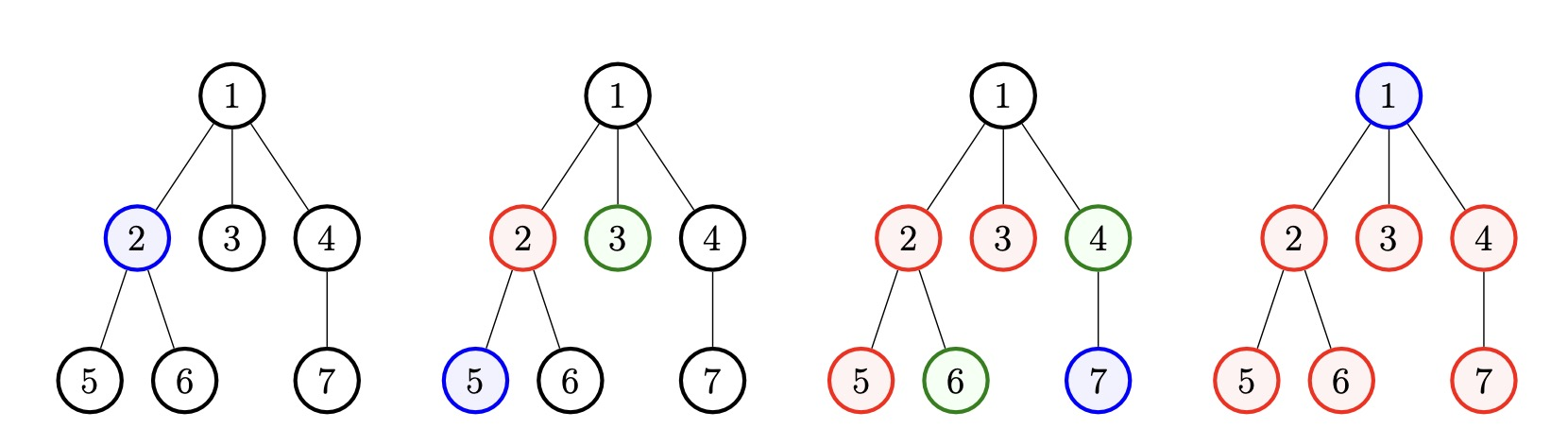Note that you are able to choose which vertices are infected by spreading and by injections.

首页