CF1650G.Counting Shortcuts

Given an undirected connected graph with $n$ vertices and $m$ edges. The graph contains no loops (edges from a vertex to itself) and multiple edges (i.e. no more than one edge between each pair of vertices). The vertices of the graph are numbered from $1$ to $n$ .

Find the number of paths from a vertex $s$ to $t$ whose length differs from the shortest path from $s$ to $t$ by no more than $1$ . It is necessary to consider all suitable paths, even if they pass through the same vertex or edge more than once (i.e. they are not simple).

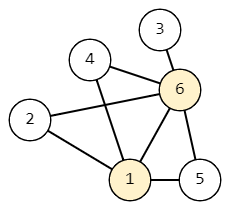Graph consisting of $6$ of vertices and $8$ of edgesFor example, let $n = 6$ , $m = 8$ , $s = 6$ and $t = 1$ , and let the graph look like the figure above. Then the length of the shortest path from $s$ to $t$ is $1$ . Consider all paths whose length is at most $1 + 1 = 2$ .

• $6 \rightarrow 1$ . The length of the path is $1$ .
• $6 \rightarrow 4 \rightarrow 1$ . Path length is $2$ .
• $6 \rightarrow 2 \rightarrow 1$ . Path length is $2$ .
• $6 \rightarrow 5 \rightarrow 1$ . Path length is $2$ .

There is a total of $4$ of matching paths.

The first line of test contains the number $t$ ( $1 \le t \le 10^4$ ) —the number of test cases in the test.

Before each test case, there is a blank line.

The first line of test case contains two numbers $n, m$ ( $2 \le n \le 2 \cdot 10^5$ , $1 \le m \le 2 \cdot 10^5$ ) —the number of vertices and edges in the graph.

The second line contains two numbers $s$ and $t$ ( $1 \le s, t \le n$ , $s \neq t$ ) —the numbers of the start and end vertices of the path.

The following $m$ lines contain descriptions of edges: the $i$ th line contains two integers $u_i$ , $v_i$ ( $1 \le u_i,v_i \le n$ ) — the numbers of vertices that connect the $i$ th edge. It is guaranteed that the graph is connected and does not contain loops and multiple edges.

It is guaranteed that the sum of values $n$ on all test cases of input data does not exceed $2 \cdot 10^5$ . Similarly, it is guaranteed that the sum of values $m$ on all test cases of input data does not exceed $2 \cdot 10^5$ .

For each test case, output a single number — the number of paths from $s$ to $t$ such that their length differs from the length of the shortest path by no more than $1$ .

Since this number may be too large, output it modulo $10^9 + 7$ .