CF1654G.Snowy Mountain

There are $n$ locations on a snowy mountain range (numbered from $1$ to $n$ ), connected by $n-1$ trails in the shape of a tree. Each trail has length $1$ . Some of the locations are base lodges. The height $h_i$ of each location is equal to the distance to the nearest base lodge (a base lodge has height $0$ ).

There is a skier at each location, each skier has initial kinetic energy $0$ . Each skier wants to ski along as many trails as possible. Suppose that the skier is skiing along a trail from location $i$ to $j$ . Skiers are not allowed to ski uphill (i.e., if $h_i < h_j$ ). It costs one unit of kinetic energy to ski along flat ground (i.e., if $h_i = h_j$ ), and a skier gains one unit of kinetic energy by skiing downhill (i.e., if $h_i > h_j$ ). For each location, compute the length of the longest sequence of trails that the skier starting at that location can ski along without their kinetic energy ever becoming negative. Skiers are allowed to visit the same location or trail multiple times.

The first line contains a single integer $n$ ( $2 \le n \le 2 \cdot 10^5$ ).

The second line contains $n$ integers $l_1, l_2, \ldots, l_n$ ( $0 \le l_i \le 1$ ). If $l_i = 1$ , location $i$ is a base lodge; if $l_i = 0$ , location $i$ is not a base lodge. It is guaranteed that there is at least $1$ base lodge.

Each of the next $n-1$ lines contains two integers $u, v$ ( $1 \leq u, v \leq n$ , $u \neq v$ ), meaning that there is a trail that connects the locations $u$ and $v$ . It is guaranteed that the given trails form a tree.

Print $n$ integers: the $i$ -th integer is equal to the length of the longest sequence of trails that the skier starting at location $i$ can ski along without their kinetic energy ever becoming negative.

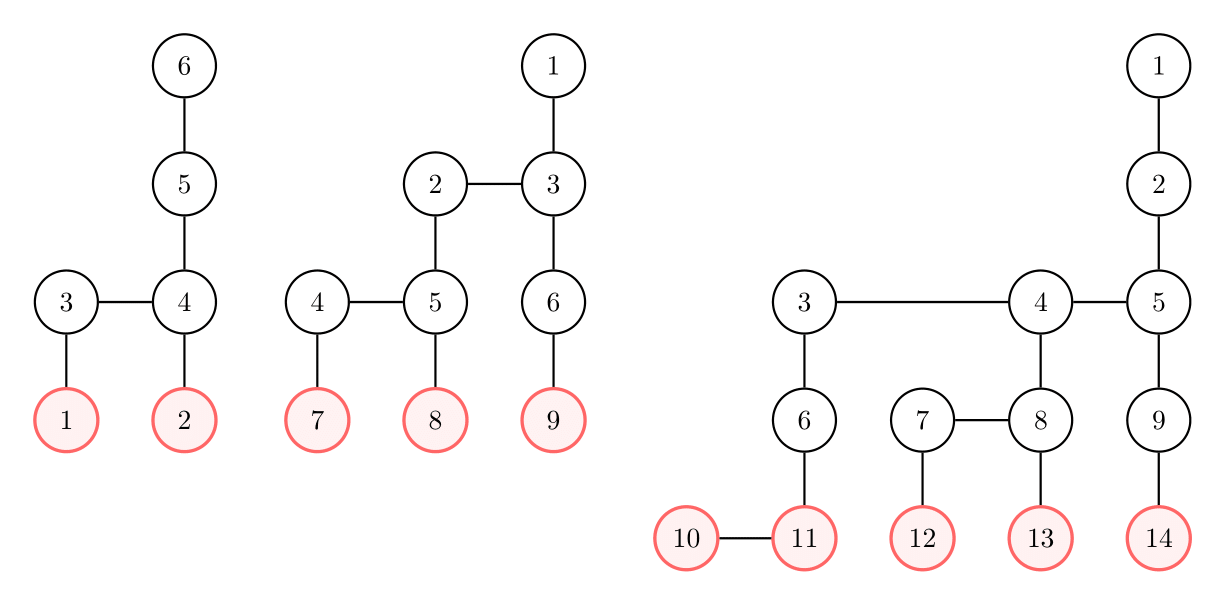
In the first test, $h = [0, 0, 1, 1, 2, 3]$ . The skier starting from $6$ can ski along at most $5$ trails, in the path $6 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 4 \rightarrow 2$ (notice that a skier can ski multiple times along the same trail and can visit more than once the same location):

• at the location $6$ , the kinetic energy is $0$ ;
• at the location $5$ , the kinetic energy increases by $1$ (because $h_5 < h_6$ ), so it becomes $1$ ;
• at the location $4$ , the kinetic energy increases by $1$ (because $h_4 < h_5$ ), so it becomes $2$ ;
• at the location $3$ , the kinetic energy decreases by $1$ (because $h_3 = h_4$ ), so it becomes $1$ ;
• at the location $4$ , the kinetic energy decreases by $1$ (because $h_4 = h_3$ ), so it becomes $0$ ;
• at the location $2$ , the kinetic energy increases by $1$ (because $h_2 < h_4$ ), so it becomes $1$ .

There isn't any sequence of trails of length greater than $5$ such that the kinetic energy is always non-negative.

Moreover,

• the optimal path for the skier starting from $1$ is $1$ (no trails);
• the optimal path for the skier starting from $2$ is $2$ (no trails);
• the optimal path for the skier starting from $3$ is $3 \rightarrow 1$ ;
• the optimal path for the skier starting from $4$ is $4 \rightarrow 2$ ;
• the optimal path for the skier starting from $5$ is $5 \rightarrow 4 \rightarrow 3 \rightarrow 1$ .

In the second test, $h = [3, 2, 2, 1, 1, 1, 0, 0, 0]$ . The skier starting from $1$ can ski along at most $5$ trails, in the path $1 \rightarrow 3 \rightarrow 2 \rightarrow 5 \rightarrow 4 \rightarrow 7$ .

• at the location $1$ , the kinetic energy is $0$ ;
• at the location $3$ , the kinetic energy increases by $1$ (because $h_3 < h_1$ ), so it becomes $1$ ;
• at the location $2$ , the kinetic energy decreases by $1$ (because $h_2 = h_3$ ), so it becomes $0$ ;
• at the location $5$ , the kinetic energy increases by $1$ (because $h_5 < h_2$ ), so it becomes $1$ ;
• at the location $4$ , the kinetic energy decreases by $1$ (because $h_4 = h_5$ ), so it becomes $0$ ;
• at the location $7$ , the kinetic energy increases by $1$ (because $h_7 < h_4$ ), so it becomes $1$ .

There isn't any sequence of trails of length greater than $5$ such that the kinetic energy is always non-negative.

In the third test, for the skier starting from vertex $1$ , the optimal path is $1 \rightarrow 2 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 6 \rightarrow 11 \rightarrow 10 \rightarrow 11$ .

Here are pictures of the first, second, and third test, with the base lodges shown in red: