CF1624G.MinOr Tree

Recently, Vlad has been carried away by spanning trees, so his friends, without hesitation, gave him a connected weighted undirected graph of $n$ vertices and $m$ edges for his birthday.

Vlad defined the ority of a spanning tree as the bitwise OR of all its weights, and now he is interested in what is the minimum possible ority that can be achieved by choosing a certain spanning tree. A spanning tree is a connected subgraph of a given graph that does not contain cycles.

In other words, you want to keep $n-1$ edges so that the graph remains connected and the bitwise OR weights of the edges are as small as possible. You have to find the minimum bitwise OR itself.

The first line of the input contains an integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases in the input.

An empty line is written in front of each test case.

This is followed by two numbers $n$ and $m$ ( $3 \le n \le 2 \cdot 10^5, n - 1 \le m \le 2 \cdot 10^5$ ) — the number of vertices and edges of the graph, respectively.

The next $m$ lines contain the description of the edges. Line $i$ contains three numbers $v_i$ , $u_i$ and $w_i$ ( $1 \le v_i, u_i \le n$ , $1 \le w_i \le 10^9$ , $v_i \neq u_i$ ) — the vertices that the edge connects and its weight.

It is guaranteed that the sum $m$ and the sum $n$ over all test cases does not exceed $2 \cdot 10^5$ and each test case contains a connected graph.

Print $t$ lines, each of which contains the answer to the corresponding set of input data — the minimum possible spanning tree ority.

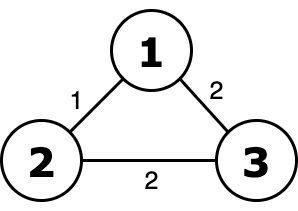Graph from the first test case. 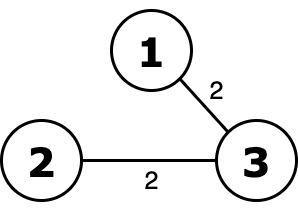Ority of this tree equals to 2 or 2 = 2 and it's minimal. 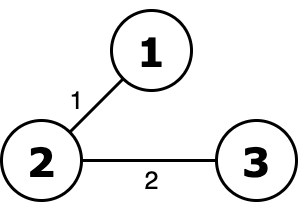Without excluding edge with weight $1$ ority is 1 or 2 = 3.