CF1625B.Elementary Particles

Martians are actively engaged in interplanetary trade. Olymp City, the Martian city known for its spaceport, has become a place where goods from all the corners of our Galaxy come. To deliver even more freight from faraway planets, Martians need fast spaceships.

A group of scientists conducts experiments to build a fast engine for the new spaceship. In the current experiment, there are $n$ elementary particles, the $i$ -th of them has type $a_i$ .

Denote a subsegment of the particle sequence ( $a_1, a_2, \dots, a_n$ ) as a sequence ( $a_l, a_{l+1}, \dots, a_r$ ) for some left bound $l$ and right bound $r$ ( $1 \le l \le r \le n$ ). For instance, the sequence $(1\ 4\ 2\ 8\ 5\ 7)$ for $l=2$ and $r=4$ has the sequence $(4\ 2\ 8)$ as a subsegment. Two subsegments are considered different if at least one bound of those subsegments differs.

Note that the subsegments can be equal as sequences but still considered different. For example, consider the sequence $(1\ 1\ 1\ 1\ 1)$ and two of its subsegments: one with $l=1$ and $r=3$ and another with $l=2$ and $r=4$ . Both subsegments are equal to $(1\ 1\ 1)$ , but still considered different, as their left and right bounds differ.

The scientists want to conduct a reaction to get two different subsegments of the same length. Denote this length $k$ . The resulting pair of subsegments must be harmonious, i. e. for some $i$ ( $1 \le i \le k$ ) it must be true that the types of particles on the $i$ -th position are the same for these two subsegments. For example, the pair $(1\ 7\ 3)$ and $(4\ 7\ 8)$ is harmonious, as both subsegments have $7$ on the second position. The pair $(1\ 2\ 3)$ and $(3\ 1\ 2)$ is not harmonious.

The longer are harmonious subsegments, the more chances for the scientists to design a fast engine. So, they asked you to calculate the maximal possible length of harmonious pair made of different subsegments.

The first line contains an integer $t$ ( $1 \le t \le 100$ ) — the number of test cases. The following are descriptions of the test cases.

The first line contains an integer $n$ ( $2 \le n \le 150\,000$ ) — the amount of elementary particles in the sequence.

The second line contains $n$ integers $a_i$ ( $1 \le a_i \le 150\,000$ ) — types of elementary particles.

It is guaranteed that the sum of $n$ over all test cases does not exceed $3\cdot10^5$ .

For each test, print a single integer, maximal possible length of harmonious pair made of different subsegments. If such pair does not exist, print $-1$ instead.

The first test case is shown on the picture below:

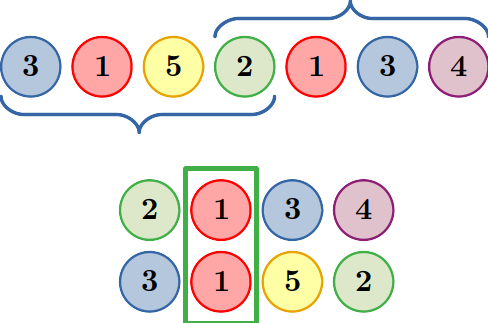As you can see from it, you may choose the subsegments $(2\ 1\ 3\ 4)$ and $(3\ 1\ 5\ 2)$ , which are a harmonious pair. Their length is equal to $4$ , so the answer is $4$ .

In the second test case, you need to take two subsegments: one with $l=1$ and $r=5$ , and one with $l=2$ and $r=6$ . It's not hard to observe that these segments are a harmonious pair and considered different even though they are both equal to $(1\ 1\ 1\ 1\ 1)$ .

In the third test case, you cannot make a harmonious pair, so the answer is $-1$ .