CF1633E.Spanning Tree Queries
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You are given a connected weighted undirected graph, consisting of n vertices and m edges.
You are asked k queries about it. Each query consists of a single integer x . For each query, you select a spanning tree in the graph. Let the weights of its edges be w1,w2,…,wn−1 . The cost of a spanning tree is i=1∑n−1∣wi−x∣ (the sum of absolute differences between the weights and x ). The answer to a query is the lowest cost of a spanning tree.
The queries are given in a compressed format. The first p (1≤p≤k) queries q1,q2,…,qp are provided explicitly. For queries from p+1 to k , qj=(qj−1⋅a+b)modc .
Print the xor of answers to all queries.
输入格式
The first line contains two integers n and m ( 2≤n≤50 ; n−1≤m≤300 ) — the number of vertices and the number of edges in the graph.
Each of the next m lines contains a description of an undirected edge: three integers v , u and w ( 1≤v,u≤n ; v=u ; 0≤w≤108 ) — the vertices the edge connects and its weight. Note that there might be multiple edges between a pair of vertices. The edges form a connected graph.
The next line contains five integers p,k,a,b and c ( 1≤p≤105 ; p≤k≤107 ; 0≤a,b≤108 ; 1≤c≤108 ) — the number of queries provided explicitly, the total number of queries and parameters to generate the queries.
The next line contains p integers q1,q2,…,qp ( 0≤qj<c ) — the first p queries.
输出格式
Print a single integer — the xor of answers to all queries.
输入输出样例
输入#1
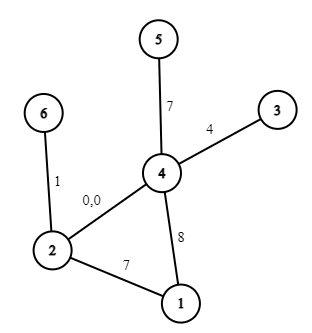
5 8 4 1 4 3 1 0 3 5 3 2 5 4 3 4 8 4 3 4 4 2 8 5 3 9 3 11 1 1 10 0 1 2
输出#1
4
输入#2
6 7 2 4 0 5 4 7 2 4 0 2 1 7 2 6 1 3 4 4 1 4 8 4 10 3 3 7 3 0 2 1
输出#2
5
输入#3
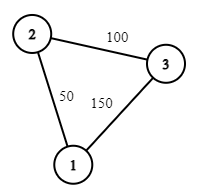
3 3 1 2 50 2 3 100 1 3 150 1 10000000 0 0 100000000 75
输出#3
164
说明/提示
The queries in the first example are 0,1,2,3,4,5,6,7,8,9,0 . The answers are 11,9,7,3,1,5,8,7,5,7,11 .
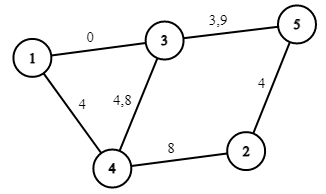 The queries in the second example are 3,0,2,1,6,0,3,5,4,1 . The answers are 14,19,15,16,11,19,14,12,13,16 .
The queries in the second example are 3,0,2,1,6,0,3,5,4,1 . The answers are 14,19,15,16,11,19,14,12,13,16 .
 The queries in the third example are 75,0,0,… . The answers are 50,150,150,… .
The queries in the third example are 75,0,0,… . The answers are 50,150,150,… .