CF1606F.Tree Queries

You are given a tree consisting of $n$ vertices. Recall that a tree is an undirected connected acyclic graph. The given tree is rooted at the vertex $1$ .

You have to process $q$ queries. In each query, you are given a vertex of the tree $v$ and an integer $k$ .

To process a query, you may delete any vertices from the tree in any order, except for the root and the vertex $v$ . When a vertex is deleted, its children become the children of its parent. You have to process a query in such a way that maximizes the value of $c(v) - m \cdot k$ (where $c(v)$ is the resulting number of children of the vertex $v$ , and $m$ is the number of vertices you have deleted). Print the maximum possible value you can obtain.

The queries are independent: the changes you make to the tree while processing a query don't affect the tree in other queries.

The first line contains one integer $n$ ( $1 \le n \le 2 \cdot 10^5$ ) — the number of vertices in the tree.

Then $n-1$ lines follow, the $i$ -th of them contains two integers $x_i$ and $y_i$ ( $1 \le x_i, y_i \le n$ ; $x_i \ne y_i$ ) — the endpoints of the $i$ -th edge. These edges form a tree.

The next line contains one integer $q$ ( $1 \le q \le 2 \cdot 10^5$ ) — the number of queries.

Then $q$ lines follow, the $j$ -th of them contains two integers $v_j$ and $k_j$ ( $1 \le v_j \le n$ ; $0 \le k_j \le 2 \cdot 10^5$ ) — the parameters of the $j$ -th query.

For each query, print one integer — the maximum value of $c(v) - m \cdot k$ you can achieve.

The tree in the first example is shown in the following picture:

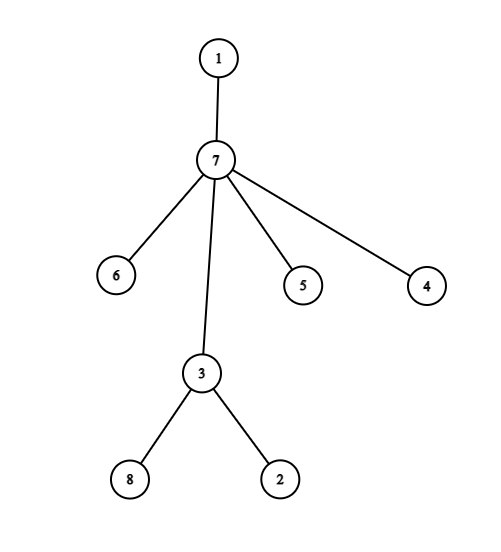Answers to the queries are obtained as follows:

1. $v=1,k=0$ : you can delete vertices $7$ and $3$ , so the vertex $1$ has $5$ children (vertices $2$ , $4$ , $5$ , $6$ , and $8$ ), and the score is $5 - 2 \cdot 0 = 5$ ;
2. $v=1,k=2$ : you can delete the vertex $7$ , so the vertex $1$ has $4$ children (vertices $3$ , $4$ , $5$ , and $6$ ), and the score is $4 - 1 \cdot 2 = 2$ .
3. $v=1,k=3$ : you shouldn't delete any vertices, so the vertex $1$ has only one child (vertex $7$ ), and the score is $1 - 0 \cdot 3 = 1$ ;
4. $v=7,k=1$ : you can delete the vertex $3$ , so the vertex $7$ has $5$ children (vertices $2$ , $4$ , $5$ , $6$ , and $8$ ), and the score is $5 - 1 \cdot 1 = 4$ ;
5. $v=5,k=0$ : no matter what you do, the vertex $5$ will have no children, so the score is $0$ ;
6. $v=7,k=200000$ : you shouldn't delete any vertices, so the vertex $7$ has $4$ children (vertices $3$ , $4$ , $5$ , and $6$ ), and the score is $4 - 0 \cdot 200000 = 4$ .