CF1610D.Not Quite Lee

Lee couldn't sleep lately, because he had nightmares. In one of his nightmares (which was about an unbalanced global round), he decided to fight back and propose a problem below (which you should solve) to balance the round, hopefully setting him free from the nightmares.

A non-empty array $b_1, b_2, \ldots, b_m$ is called good, if there exist $m$ integer sequences which satisfy the following properties:

• The $i$ -th sequence consists of $b_i$ consecutive integers (for example if $b_i = 3$ then the $i$ -th sequence can be $(-1, 0, 1)$ or $(-5, -4, -3)$ but not $(0, -1, 1)$ or $(1, 2, 3, 4)$ ).
• Assuming the sum of integers in the $i$ -th sequence is $sum_i$ , we want $sum_1 + sum_2 + \ldots + sum_m$ to be equal to $0$ .

You are given an array $a_1, a_2, \ldots, a_n$ . It has $2^n - 1$ nonempty subsequences. Find how many of them are good.

As this number can be very large, output it modulo $10^9 + 7$ .

An array $c$ is a subsequence of an array $d$ if $c$ can be obtained from $d$ by deletion of several (possibly, zero or all) elements.

The first line contains a single integer $n$ ( $2 \le n \le 2 \cdot 10^5$ ) — the size of array $a$ .

The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ( $1 \le a_i \le 10^9$ ) — elements of the array.

Print a single integer — the number of nonempty good subsequences of $a$ , modulo $10^9 + 7$ .

For the first test, two examples of good subsequences are $[2, 7]$ and $[2, 2, 4, 7]$ :

For $b = [2, 7]$ we can use $(-3, -4)$ as the first sequence and $(-2, -1, \ldots, 4)$ as the second. Note that subsequence $[2, 7]$ appears twice in $[2, 2, 4, 7]$ , so we have to count it twice.

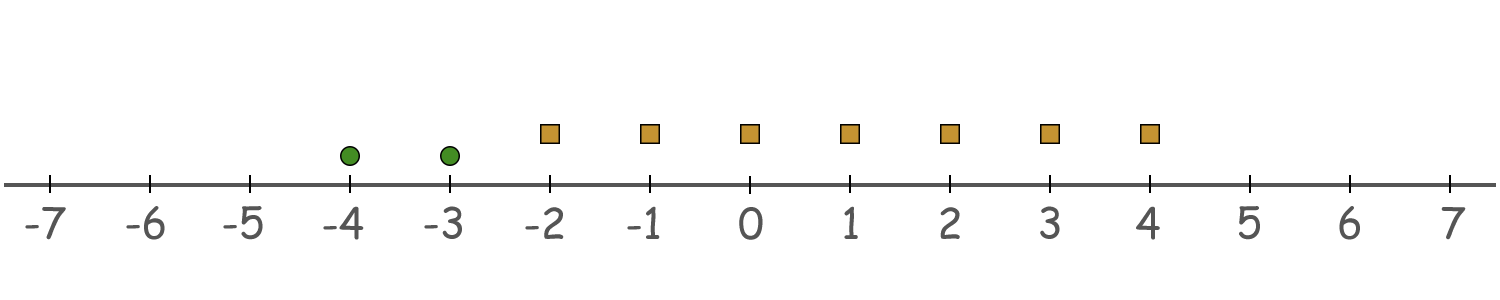Green circles denote $(-3, -4)$ and orange squares denote $(-2, -1, \ldots, 4)$ .For $b = [2, 2, 4, 7]$ the following sequences would satisfy the properties: $(-1, 0)$ , $(-3, -2)$ , $(0, 1, 2, 3)$ and $(-3, -2, \ldots, 3)$