CF1583H.Omkar and Tours

Omkar is hosting tours of his country, Omkarland! There are $n$ cities in Omkarland, and, rather curiously, there are exactly $n-1$ bidirectional roads connecting the cities to each other. It is guaranteed that you can reach any city from any other city through the road network.

Every city has an enjoyment value $e$ . Each road has a capacity $c$ , denoting the maximum number of vehicles that can be on it, and an associated toll $t$ . However, the toll system in Omkarland has an interesting quirk: if a vehicle travels on multiple roads on a single journey, they pay only the highest toll of any single road on which they traveled. (In other words, they pay $\max t$ over all the roads on which they traveled.) If a vehicle traverses no roads, they pay $0$ toll.

Omkar has decided to host $q$ tour groups. Each tour group consists of $v$ vehicles starting at city $x$ . (Keep in mind that a tour group with $v$ vehicles can travel only on roads with capacity $\geq v$ .) Being the tour organizer, Omkar wants his groups to have as much fun as they possibly can, but also must reimburse his groups for the tolls that they have to pay. Thus, for each tour group, Omkar wants to know two things: first, what is the enjoyment value of the city $y$ with maximum enjoyment value that the tour group can reach from their starting city, and second, how much per vehicle will Omkar have to pay to reimburse the entire group for their trip from $x$ to $y$ ? (This trip from $x$ to $y$ will always be on the shortest path from $x$ to $y$ .)

In the case that there are multiple reachable cities with the maximum enjoyment value, Omkar will let his tour group choose which one they want to go to. Therefore, to prepare for all possible scenarios, he wants to know the amount of money per vehicle that he needs to guarantee that he can reimburse the group regardless of which city they choose.

The first line contains two integers $n$ and $q$ ( $2 \leq n \leq 2 \cdot 10^5$ , $1 \leq q \leq 2 \cdot 10^5$ ), representing the number of cities and the number of groups, respectively.

The next line contains $n$ integers $e_1, e_2, \ldots, e_n$ ( $1 \leq e_i \leq 10^9$ ), where $e_i$ represents the enjoyment value for city $i$ .

The next $n-1$ lines each contain four integers $a$ , $b$ , $c$ , and $t$ ( $1 \leq a,b \leq n$ , $1 \leq c \leq 10^9$ , $1 \leq t \leq 10^9$ ), representing an road between city $a$ and city $b$ with capacity $c$ and toll $t$ .

The next $q$ lines each contain two integers $v$ and $x$ ( $1 \leq v \leq 10^9$ , $1 \leq x \leq n$ ), representing the number of vehicles in the tour group and the starting city, respectively.

Output $q$ lines. The $i$ -th line should contain two integers: the highest possible enjoyment value of a city reachable by the $i$ -th tour group, and the amount of money per vehicle Omkar needs to guarantee that he can reimburse the $i$ -th tour group.

A map of the first sample is shown below. For the nodes, unbolded numbers represent indices and bolded numbers represent enjoyment values. For the edges, unbolded numbers represent capacities and bolded numbers represent tolls.

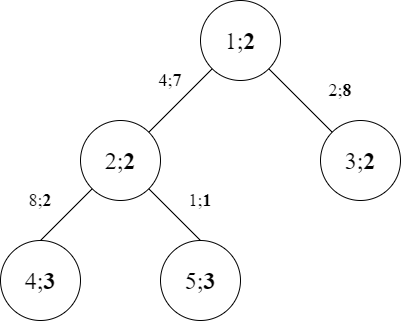For the first query, a tour group of size $1$ starting at city $3$ can reach cities $1$ , $2$ , $3$ , $4$ , and $5$ . Thus, the largest enjoyment value that they can reach is $3$ . If the tour group chooses to go to city $4$ , Omkar will have to pay $8$ per vehicle, which is the maximum.

For the second query, a tour group of size $9$ starting at city $5$ can reach only city $5$ . Thus, the largest reachable enjoyment value is still $3$ , and Omkar will pay $0$ per vehicle.

For the third query, a tour group of size $6$ starting at city $2$ can reach cities $2$ and $4$ . The largest reachable enjoyment value is again $3$ . If the tour group chooses to go to city $4$ , Omkar will have to pay $2$ per vehicle, which is the maximum.

A map of the second sample is shown below:

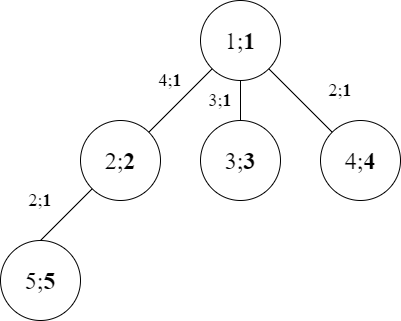For the first query, a tour group of size $5$ starting at city $1$ can only reach city $1$ . Thus, their maximum enjoyment value is $1$ and the cost Omkar will have to pay is $0$ per vehicle.

For the second query, a tour group of size $4$ starting at city $1$ can reach cities $1$ and $2$ . Thus, their maximum enjoyment value is $2$ and Omkar will pay $1$ per vehicle.

For the third query, a tour group of size $3$ starting at city $1$ can reach cities $1$ , $2$ , and $3$ . Thus, their maximum enjoyment value is $3$ and Omkar will pay $1$ per vehicle.

For the fourth query, a tour group of size $2$ starting at city $1$ can reach cities $1$ , $2$ , $3$ and $4$ . Thus, their maximum enjoyment value is $4$ and Omkar will pay $1$ per vehicle.

For the fifth query, a tour group of size $1$ starting at city $1$ can reach cities $1$ , $2$ , $3$ , $4$ , and $5$ . Thus, their maximum enjoyment value is $5$ and Omkar will pay $1$ per vehicle.