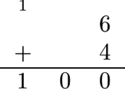CF1567C.Carrying Conundrum

Alice has just learned addition. However, she hasn't learned the concept of "carrying" fully — instead of carrying to the next column, she carries to the column two columns to the left.

For example, the regular way to evaluate the sum $2039 + 2976$ would be as shown:

However, Alice evaluates it as shown:

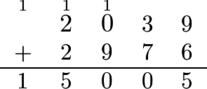In particular, this is what she does:

• add $9$ and $6$ to make $15$ , and carry the $1$ to the column two columns to the left, i. e. to the column " $0$ $9$ ";
• add $3$ and $7$ to make $10$ and carry the $1$ to the column two columns to the left, i. e. to the column " $2$ $2$ ";
• add $1$ , $0$ , and $9$ to make $10$ and carry the $1$ to the column two columns to the left, i. e. to the column above the plus sign;
• add $1$ , $2$ and $2$ to make $5$ ;
• add $1$ to make $1$ .

Thus, she ends up with the incorrect result of $15005$ .Alice comes up to Bob and says that she has added two numbers to get a result of $n$ . However, Bob knows that Alice adds in her own way. Help Bob find the number of ordered pairs of positive integers such that when Alice adds them, she will get a result of $n$ . Note that pairs $(a, b)$ and $(b, a)$ are considered different if $a \ne b$ .

The input consists of multiple test cases. The first line contains an integer $t$ ( $1 \leq t \leq 1000$ ) — the number of test cases. The description of the test cases follows.

The only line of each test case contains an integer $n$ ( $2 \leq n \leq 10^9$ ) — the number Alice shows Bob.

For each test case, output one integer — the number of ordered pairs of positive integers such that when Alice adds them, she will get a result of $n$ .

In the first test case, when Alice evaluates any of the sums $1 + 9$ , $2 + 8$ , $3 + 7$ , $4 + 6$ , $5 + 5$ , $6 + 4$ , $7 + 3$ , $8 + 2$ , or $9 + 1$ , she will get a result of $100$ . The picture below shows how Alice evaluates $6 + 4$ :