CF1569E.Playoff Restoration

$2^k$ teams participate in a playoff tournament. The tournament consists of $2^k - 1$ games. They are held as follows: first of all, the teams are split into pairs: team $1$ plays against team $2$ , team $3$ plays against team $4$ (exactly in this order), and so on (so, $2^{k-1}$ games are played in that phase). When a team loses a game, it is eliminated, and each game results in elimination of one team (there are no ties). After that, only $2^{k-1}$ teams remain. If only one team remains, it is declared the champion; otherwise, $2^{k-2}$ games are played: in the first one of them, the winner of the game " $1$ vs $2$ " plays against the winner of the game " $3$ vs $4$ ", then the winner of the game " $5$ vs $6$ " plays against the winner of the game " $7$ vs $8$ ", and so on. This process repeats until only one team remains.

After the tournament ends, the teams are assigned places according to the tournament phase when they were eliminated. In particular:

• the winner of the tournament gets place $1$ ;
• the team eliminated in the finals gets place $2$ ;
• both teams eliminated in the semifinals get place $3$ ;
• all teams eliminated in the quarterfinals get place $5$ ;
• all teams eliminated in the 1/8 finals get place $9$ , and so on.

For example, this picture describes one of the possible ways the tournament can go with $k = 3$ , and the resulting places of the teams:

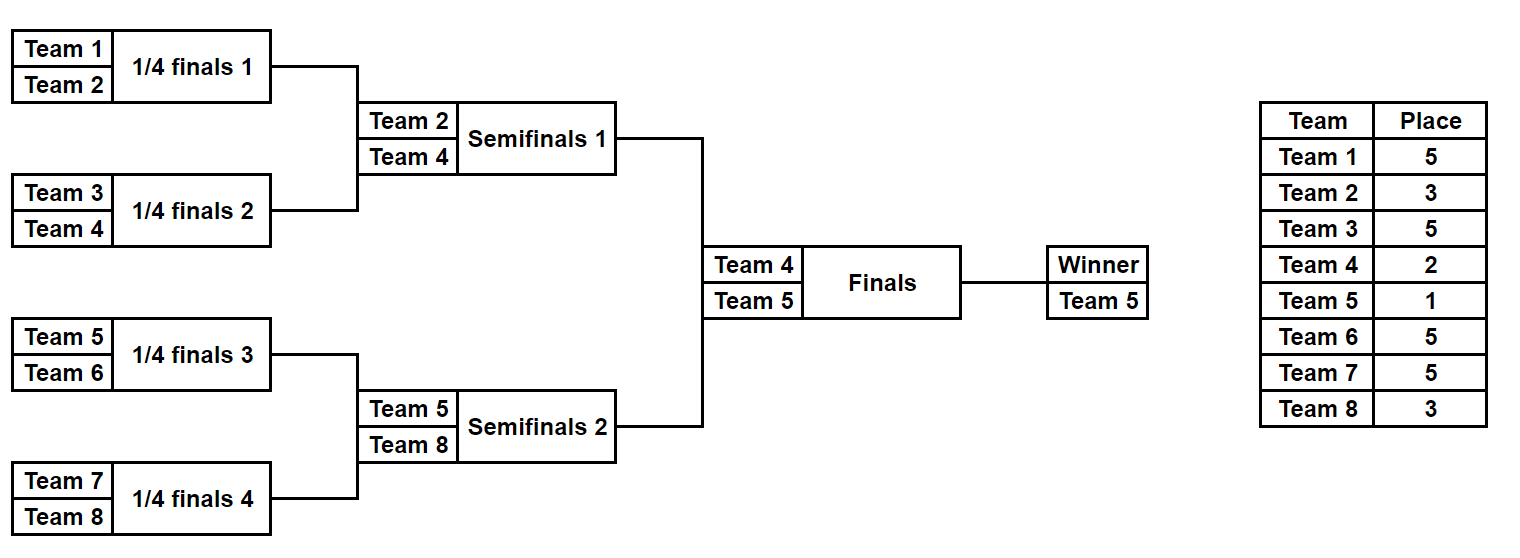After a tournament which was conducted by the aforementioned rules ended, its results were encoded in the following way. Let $p_i$ be the place of the $i$ -th team in the tournament. The hash value of the tournament $h$ is calculated as $h = (\sum \limits_{i=1}^{2^k} i \cdot A^{p_i}) \bmod 998244353$ , where $A$ is some given integer.

Unfortunately, due to a system crash, almost all tournament-related data was lost. The only pieces of data that remain are the values of $k$ , $A$ and $h$ . You are asked to restore the resulting placing of the teams in the tournament, if it is possible at all.

The only line contains three integers $k$ , $A$ and $h$ ( $1 \le k \le 5$ ; $100 \le A \le 10^8$ ; $0 \le h \le 998244352$ ).

If it is impossible to find any placing of the teams that is consistent with the data you have, print one integer $-1$ .

Otherwise, print $2^k$ integers, where $i$ -th integer should be equal to $p_i$ (the place of the $i$ -th team). Note that your answer should be consistent with one of the possible ways the tournament could go, and note that the initial structure of the tournament is fixed (for example, teams $1$ and $2$ always play in the first phase of the tournament against each other). If there are multiple ways to restore the places of the teams which are consistent with the data you have, print any of them.

The tournament for the first example is described in the statement.

For the third example, the placing $[1, 2, 3, 3]$ (team $1$ gets place $1$ , team $2$ gets place $2$ , teams $3$ and $4$ get place $3$ ) could result in a hash value of $7020100$ with $A = 100$ , but no tournament can result in such placing since teams $1$ and $2$ play against each other in the semifinals, so they cannot get two first places.