CF1575B.Building an Amusement Park

Mr. Chanek lives in a city represented as a plane. He wants to build an amusement park in the shape of a circle of radius $r$ . The circle must touch the origin (point $(0, 0)$ ).

There are $n$ bird habitats that can be a photo spot for the tourists in the park. The $i$ -th bird habitat is at point $p_i = (x_i, y_i)$ .

Find the minimum radius $r$ of a park with at least $k$ bird habitats inside.

A point is considered to be inside the park if and only if the distance between $p_i$ and the center of the park is less than or equal to the radius of the park. Note that the center and the radius of the park do not need to be integers.

In this problem, it is guaranteed that the given input always has a solution with $r \leq 2 \cdot 10^5$ .

The first line contains two integers $n$ and $k$ ( $1 \leq n \leq 10^5$ , $1 \leq k \leq n$ ) — the number of bird habitats in the city and the number of bird habitats required to be inside the park.

The $i$ -th of the next $n$ lines contains two integers $x_i$ and $y_i$ ( $0 \leq |x_i|, |y_i| \leq 10^5$ ) — the position of the $i$ -th bird habitat.

Output a single real number $r$ denoting the minimum radius of a park with at least $k$ bird habitats inside. It is guaranteed that the given input always has a solution with $r \leq 2 \cdot 10^5$ .

Your answer is considered correct if its absolute or relative error does not exceed $10^{-4}$ .

Formally, let your answer be $a$ , and the jury's answer be $b$ . Your answer is accepted if and only if $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4}$ .

In the first example, Mr. Chanek can put the center of the park at $(-3, -1)$ with radius $\sqrt{10} \approx 3.162$ . It can be proven this is the minimum $r$ .

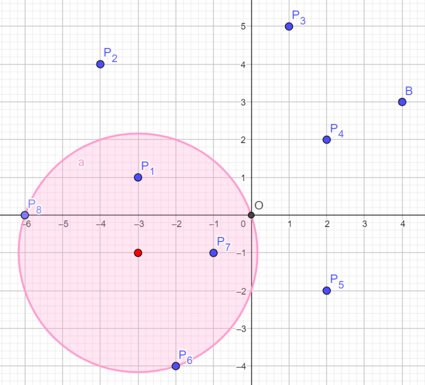
The following illustrates the first example. The blue points represent bird habitats and the red circle represents the amusement park.