CF1575K.Knitting Batik

Mr. Chanek wants to knit a batik, a traditional cloth from Indonesia. The cloth forms a grid $a$ with size $n \times m$ . There are $k$ colors, and each cell in the grid can be one of the $k$ colors.

Define a sub-rectangle as an ordered pair of two cells $((x_1, y_1), (x_2, y_2))$ , denoting the top-left cell and bottom-right cell (inclusively) of a sub-rectangle in $a$ . Two sub-rectangles $((x_1, y_1), (x_2, y_2))$ and $((x_3, y_3), (x_4, y_4))$ have the same pattern if and only if the following holds:

• they have the same width ( $x_2 - x_1 = x_4 - x_3$ );
• they have the same height ( $y_2 - y_1 = y_4 - y_3$ );
• for every pair $(i, j)$ where $0 \leq i \leq x_2 - x_1$ and $0 \leq j \leq y_2 - y_1$ , the color of cells $(x_1 + i, y_1 + j)$ and $(x_3 + i, y_3 + j)$ are equal.

Count the number of possible batik color combinations, such that the subrectangles $((a_x, a_y),(a_x + r - 1, a_y + c - 1))$ and $((b_x, b_y),(b_x + r - 1, b_y + c - 1))$ have the same pattern.

Output the answer modulo $10^9 + 7$ .

The first line contains five integers $n$ , $m$ , $k$ , $r$ , and $c$ ( $1 \leq n, m \leq 10^9$ , $1 \leq k \leq 10^9$ , $1 \leq r \leq \min(10^6, n)$ , $1 \leq c \leq \min(10^6, m)$ ) — the size of the batik, the number of colors, and size of the sub-rectangle.

The second line contains four integers $a_x$ , $a_y$ , $b_x$ , and $b_y$ ( $1 \leq a_x, b_x \leq n$ , $1 \leq a_y, b_y \leq m$ ) — the top-left corners of the first and second sub-rectangle. Both of the sub-rectangles given are inside the grid ( $1 \leq a_x + r - 1$ , $b_x + r - 1 \leq n$ , $1 \leq a_y + c - 1$ , $b_y + c - 1 \leq m$ ).

Output an integer denoting the number of possible batik color combinations modulo $10^9 + 7$ .

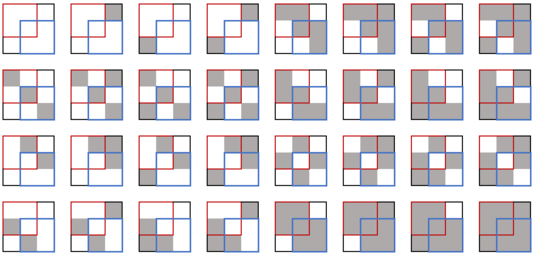
The following are all $32$ possible color combinations in the first example.