CF1575M.Managing Telephone Poles

Mr. Chanek's city can be represented as a plane. He wants to build a housing complex in the city.

There are some telephone poles on the plane, which is represented by a grid $a$ of size $(n + 1) \times (m + 1)$ . There is a telephone pole at $(x, y)$ if $a_{x, y} = 1$ .

For each point $(x, y)$ , define $S(x, y)$ as the square of the Euclidean distance between the nearest pole and $(x, y)$ . Formally, the square of the Euclidean distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $(x_2 - x_1)^2 + (y_2 - y_1)^2$ .

To optimize the building plan, the project supervisor asks you the sum of all $S(x, y)$ for each $0 \leq x \leq n$ and $0 \leq y \leq m$ . Help him by finding the value of $\sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}}$ .

The first line contains two integers $n$ and $m$ ( $0 \leq n, m < 2000$ ) — the size of the grid.

Then $(n + 1)$ lines follow, each containing $(m + 1)$ integers $a_{i, j}$ ( $0 \leq a_{i, j} \leq 1$ ) — the grid denoting the positions of telephone poles in the plane. There is at least one telephone pole in the given grid.

Output an integer denoting the value of $\sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}}$ .

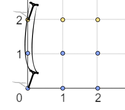In the first example, the nearest telephone pole for the points $(0,0)$ , $(1,0)$ , $(2,0)$ , $(0,1)$ , $(1,1)$ , and $(2,1)$ is at $(0, 0)$ . While the nearest telephone pole for the points $(0, 2)$ , $(1,2)$ , and $(2,2)$ is at $(0, 2)$ . Thus, $\sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} = (0 + 1 + 4) + (1 + 2 + 5) + (0 + 1 + 4) = 18$ .