CF1578D.Dragon Curve

A dragon curve is a self-similar fractal curve. In this problem, it is a curve that consists of straight-line segments of the same length connected at right angles. A simple way to construct a dragon curve is as follows: take a strip of paper, fold it in half $n$ times in the same direction, then partially unfold it such that the segments are joined at right angles. This is illustrated here:

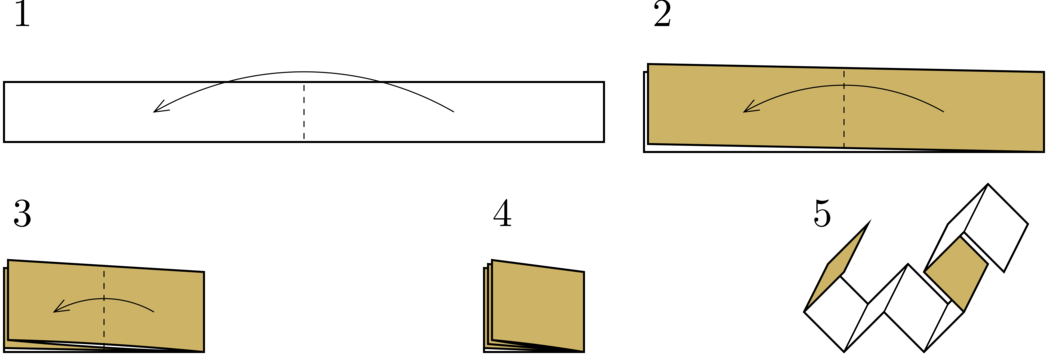In this example, a dragon curve of order $3$ is constructed. In general, a dragon curve of a higher order will have a dragon curve of a lower order as its prefix. This allows us to define a dragon curve of infinite order, which is the limit of dragon curves of a finite order as the order approaches infinity.

Consider four dragon curves of infinite order. Each starts at the origin (the point $(0,0)$ ), and the length of each segment is $\sqrt2$ . The first segments of the curves end at the points $(1,1)$ , $(-1,1)$ , $(-1,-1)$ and $(1,-1)$ , respectively. The first turn of each curve is left (that is, the second segment of the first curve ends at the point $(0,2)$ ). In this case, every segment is a diagonal of an axis-aligned unit square with integer coordinates, and it can be proven that there is exactly one segment passing through every such square.

Given a point $(x,y)$ , your task is to find on which of the four curves lies the segment passing through the square with the opposite corners at $(x,y)$ and $(x+1,y+1)$ , as well as the position of that segment on that curve. The curves are numbered $1$ through $4$ . Curve $1$ goes through $(1,1)$ , $2$ through $(-1,1)$ , $3$ through $(-1,-1)$ , and $4$ through $(1,-1)$ . The segments are numbered starting with $1$ .

The first line contains an integer $n$ ( $1\le n\le2\cdot10^5$ ) — the number of test cases.

Each of the following $n$ lines contains two integers $x$ and $y$ ( $-10^9\le x,y\le10^9$ ) — the coordinates.

For each test case, print a line containing two integers — the first is the index of the curve (an integer between $1$ and $4$ , inclusive), and the second is the position on the curve (the first segment has the position $1$ ).

You can use this illustration to debug your solution: