CF1578J.Just Kingdom

The Just Kingdom is ruled by a king and his $n$ lords, numbered $1$ to $n$ . Each of the lords is a vassal of some overlord, who might be the king himself, or a different lord closer to the king. The king, and all his lords, are just and kind.

Each lord has certain needs, which can be expressed as a certain amount of money they need. However, if a lord, or the king, receives any money, they will first split it equally between all their vassals who still have unmet needs. Only if all the needs of all their vassals are met, they will take the money to fulfill their own needs. If there is any money left over, they will return the excess to their overlord (who follows the standard procedure for distributing money).

At the beginning of the year, the king receives a certain sum of tax money and proceeds to split it according to the rules above. If the amount of tax money is greater than the total needs of all the lords, the procedure guarantees everybody's needs will be fulfilled, and the excess money will be left with the king. However, if there is not enough money, some lords will not have their needs met.

For each lord, determine the minimum amount of tax money the king has to receive so that this lord's needs are met.

The first line of the input contains the number of lords $n$ ( $0 \le n \le 3 \cdot 10^5$ ). Each of the next $n$ lines describes one of the lords. The $i$ -th line contains two integers: $o_i$ ( $0 \le o_i < i$ ) — the index of the overlord of the $i$ -th lord (with zero meaning the king is the overlord), and $m_i$ ( $1 \le m_i \le 10^6$ ) — the amount of money the $i$ -th lord needs.

Print $n$ integer numbers $t_i$ . The $i$ -th number should be the minimum integer amount of tax money the king has to receive for which the needs of the $i$ -th lord will be met.

In the sample input, if the king receives $5$ units of tax money, he will split it equally between his vassals — the lords $1$ , $3$ , and $5$ , with each receiving $\frac{5}{3}$ of money.

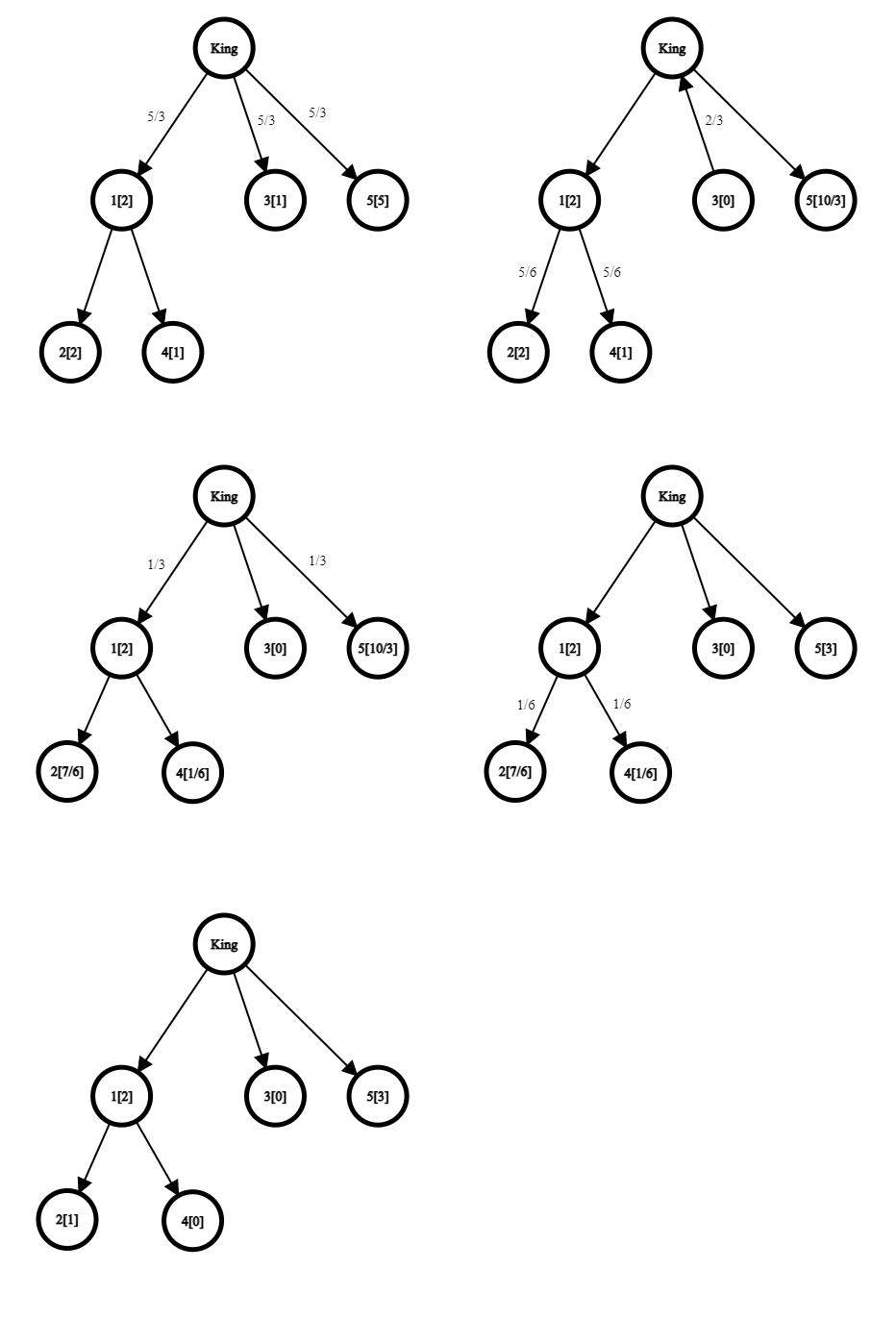Lord $1$ will split the money equally between his vassals — $2$ and $4$ , with each receiving $\frac{5}{6}$ . Lord $5$ will keep the money (having no vassals). Lord $3$ will keep $1$ unit of money, and give the remaining $\frac{2}{3}$ to the king. The king will then split the $\frac{2}{3}$ between the vassals with unmet needs — $1$ and $5$ , passing $\frac{1}{3}$ to each. Lord $5$ will keep the extra cash (now having a total of $2$ , still not enough to meet his needs). Lord $1$ will split it equally between his vassals, and the extra $\frac{1}{6}$ will be enough to meet the needs of lord $4$ .