CF1543E.The Final Pursuit

Finally, you have defeated Razor and now, you are the Most Wanted street racer. Sergeant Cross has sent the full police force after you in a deadly pursuit. Fortunately, you have found a hiding spot but you fear that Cross and his force will eventually find you. To increase your chances of survival, you want to tune and repaint your BMW M3 GTR.

The car can be imagined as a permuted $n$ -dimensional hypercube. A simple $n$ -dimensional hypercube is an undirected unweighted graph built recursively as follows:

• Take two simple $(n-1)$ -dimensional hypercubes one having vertices numbered from $0$ to $2^{n-1}-1$ and the other having vertices numbered from $2^{n-1}$ to $2^{n}-1$ . A simple $0$ -dimensional Hypercube is just a single vertex.
• Add an edge between the vertices $i$ and $i+2^{n-1}$ for each $0\leq i < 2^{n-1}$ .

A permuted $n$ -dimensional hypercube is formed by permuting the vertex numbers of a simple $n$ -dimensional hypercube in any arbitrary manner.

Examples of a simple and permuted $3$ -dimensional hypercubes are given below:

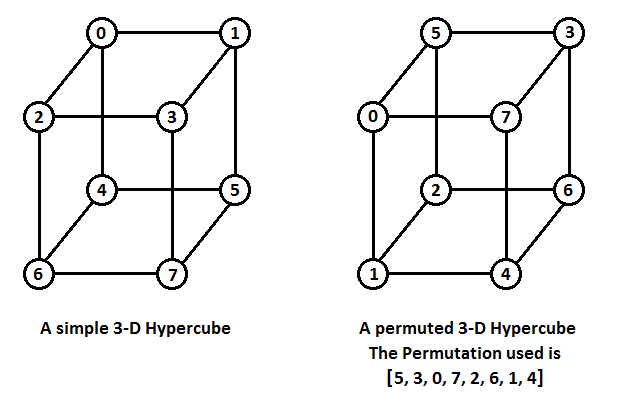Note that a permuted $n$ -dimensional hypercube has the following properties:

• There are exactly $2^n$ vertices.
• There are exactly $n\cdot 2^{n-1}$ edges.
• Each vertex is connected to exactly $n$ other vertices.
• There are no self-loops or duplicate edges.

Let's denote the permutation used to generate the permuted $n$ -dimensional hypercube, representing your car, from a simple $n$ -dimensional hypercube by $P$ . Before messing up the functionalities of the car, you want to find this permutation so that you can restore the car if anything goes wrong. But the job isn't done yet.

You have $n$ different colours numbered from $0$ to $n-1$ . You want to colour the vertices of this permuted $n$ -dimensional hypercube in such a way that for each and every vertex $u$ satisfying $0\leq u < 2^n$ and for each and every colour $c$ satisfying $0\leq c < n$ , there is at least one vertex $v$ adjacent to $u$ having a colour $c$ . In other words, from each and every vertex, it must be possible to reach a vertex of any colour by just moving to an adjacent vertex.

Given the permuted $n$ -dimensional hypercube, find any valid permutation $P$ and colouring.

The first line of input contains a single integer $t$ ( $1\leq t\leq 4096$ ) — the number of test cases.

For each test case, the first line contains a single integer $n$ ( $1\leq n\leq 16$ ).

Each of the next $n\cdot 2^{n-1}$ lines contain two integers $u$ and $v$ ( $0\leq u, v < 2^n$ ) denoting that there is an edge between the vertices numbered $u$ and $v$ .

It is guaranteed that the graph described in the input is a permuted $n$ -dimensional hypercube.

Additionally, it is guaranteed that the sum of $2^n$ over all test cases does not exceed $2^{16}=65\,536$ .

For each test case, print two lines.

In the first line, output any permutation $P$ of length $2^n$ that can be used to transform a simple $n$ -dimensional hypercube to the permuted $n$ -dimensional hypercube given in the input. Two permuted hypercubes are considered the same if they have the same set of edges. If there are multiple answers, output any of them.

In the second line, print the colouring. If there is no way to colour the vertices satisfying the conditions, output $-1$ . Otherwise, output a single line containing $2^n$ space separated integers. The $i$ -th integer must be the colour of the vertex numbered $(i-1)$ in the permuted $n$ -dimensional hypercube. If there are multiple answers, output any of them.

The colouring and the permuted hypercube for the first test case is shown below:

The colouring and the permuted hypercube for the second test case is shown below:

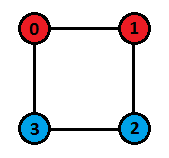The permuted hypercube for the third test case is given in the problem statement. However, it can be shown that there exists no way to colour that cube satifying all the conditions. Note that some other permutations like $[0, 5, 7, 3, 1, 2, 4, 6]$ and $[0, 1, 5, 2, 7, 4, 3, 6]$ will also give the same permuted hypercube.