CF1556F.Sports Betting

William is not only interested in trading but also in betting on sports matches. $n$ teams participate in each match. Each team is characterized by strength $a_i$ . Each two teams $i < j$ play with each other exactly once. Team $i$ wins with probability $\frac{a_i}{a_i + a_j}$ and team $j$ wins with probability $\frac{a_j}{a_i + a_j}$ .

The team is called a winner if it directly or indirectly defeated all other teams. Team $a$ defeated (directly or indirectly) team $b$ if there is a sequence of teams $c_1$ , $c_2$ , ... $c_k$ such that $c_1 = a$ , $c_k = b$ and team $c_i$ defeated team $c_{i + 1}$ for all $i$ from $1$ to $k - 1$ . Note that it is possible that team $a$ defeated team $b$ and in the same time team $b$ defeated team $a$ .

William wants you to find the expected value of the number of winners.

The first line contains a single integer $n$ ( $1 \leq n \leq 14$ ), which is the total number of teams participating in a match.

The second line contains $n$ integers $a_1, a_2, \dots, a_n$ ( $1 \leq a_i \leq 10^6$ ) — the strengths of teams participating in a match.

Output a single integer — the expected value of the number of winners of the tournament modulo $10^9 + 7$ .

Formally, let $M = 10^9+7$ . It can be demonstrated that the answer can be presented as a irreducible fraction $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \not \equiv 0 \pmod{M}$ . Output a single integer equal to $p \cdot q^{-1} \bmod M$ . In other words, output an integer $x$ such that $0 \le x < M$ and $x \cdot q \equiv p \pmod{M}$ .

To better understand in which situation several winners are possible let's examine the second test:

One possible result of the tournament is as follows ( $a \rightarrow b$ means that $a$ defeated $b$ ):

• $1 \rightarrow 2$
• $2 \rightarrow 3$
• $3 \rightarrow 1$
• $1 \rightarrow 4$
• $1 \rightarrow 5$
• $2 \rightarrow 4$
• $2 \rightarrow 5$
• $3 \rightarrow 4$
• $3 \rightarrow 5$
• $4 \rightarrow 5$

Or more clearly in the picture:

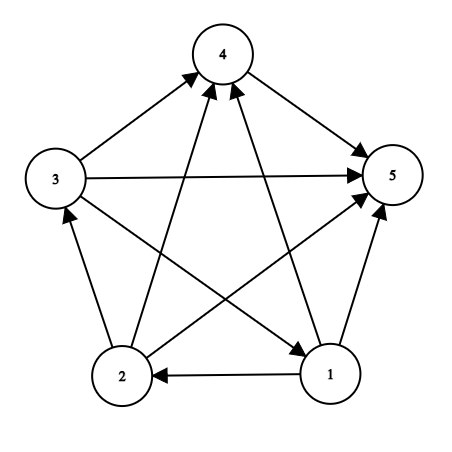In this case every team from the set $\{ 1, 2, 3 \}$ directly or indirectly defeated everyone. I.e.:

• $1$ st defeated everyone because they can get to everyone else in the following way $1 \rightarrow 2$ , $1 \rightarrow 2 \rightarrow 3$ , $1 \rightarrow 4$ , $1 \rightarrow 5$ .
• $2$ nd defeated everyone because they can get to everyone else in the following way $2 \rightarrow 3$ , $2 \rightarrow 3 \rightarrow 1$ , $2 \rightarrow 4$ , $2 \rightarrow 5$ .
• $3$ rd defeated everyone because they can get to everyone else in the following way $3 \rightarrow 1$ , $3 \rightarrow 1 \rightarrow 2$ , $3 \rightarrow 4$ , $3 \rightarrow 5$ .

Therefore the total number of winners is $3$ .