CF1527D.MEX Tree

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

You are given a tree with $n$ nodes, numerated from $0$ to $n-1$ . For each $k$ between $0$ and $n$ , inclusive, you have to count the number of unordered pairs $(u,v)$ , $u \neq v$ , such that the MEX of all the node labels in the shortest path from $u$ to $v$ (including end points) is $k$ .

The MEX of a sequence of integers is the smallest non-negative integer that does not belong to the sequence.

输入格式

The first line contains a single integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases.

The first line of each test case contains a single integer $n$ ( $2 \le n \le 2 \cdot 10^{5}$ ).

The next $n-1$ lines of each test case describe the tree that has to be constructed. These lines contain two integers $u$ and $v$ ( $0 \le u,v \le n-1$ ) denoting an edge between $u$ and $v$ ( $u \neq v$ ).

It is guaranteed that the given edges form a tree.

It is also guaranteed that the sum of $n$ for all test cases does not exceed $2 \cdot 10^{5}$ .

输出格式

For each test case, print $n+1$ integers: the number of paths in the tree, such that the MEX of all the node labels in that path is $k$ for each $k$ from $0$ to $n$ .

输入输出样例

输入#1
```
2
4
0 1
0 2
2 3
2
1 0
```
输出#1
```
1 2 1 1 1 
0 0 1
```

说明/提示

In example case $1$ ,

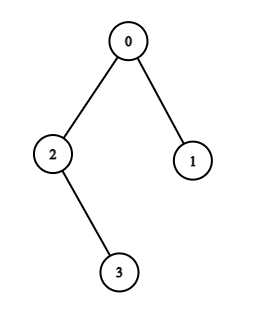
For $k = 0$ , there is $1$ path that is from $2$ to $3$ as $MEX([2, 3]) = 0$ .
For $k = 1$ , there are $2$ paths that is from $0$ to $2$ as $MEX([0, 2]) = 1$ and $0$ to $3$ as $MEX([0, 2, 3]) = 1$ .
For $k = 2$ , there is $1$ path that is from $0$ to $1$ as $MEX([0, 1]) = 2$ .
For $k = 3$ , there is $1$ path that is from $1$ to $2$ as $MEX([1, 0, 2]) = 3$
For $k = 4$ , there is $1$ path that is from $1$ to $3$ as $MEX([1, 0, 2, 3]) = 4$ .

In example case $2$ ,

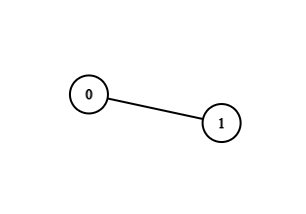
For $k = 0$ , there are no such paths.
For $k = 1$ , there are no such paths.
For $k = 2$ , there is $1$ path that is from $0$ to $1$ as $MEX([0, 1]) = 2$ .

首页