CF1534B.Histogram Ugliness

Little Dormi received a histogram with $n$ bars of height $a_1, a_2, \ldots, a_n$ for Christmas. However, the more he played with his new histogram, the more he realized its imperfections, so today he wanted to modify it to his liking.

To modify the histogram, Little Dormi is able to perform the following operation an arbitrary number of times:

• Select an index $i$ ( $1 \le i \le n$ ) where $a_i>0$ , and assign $a_i := a_i-1$ .

Little Dormi defines the ugliness score of his histogram (after performing some number of operations) as the sum of the vertical length of its outline and the number of operations he performed on it. And to make the histogram as perfect as possible, he would like to minimize the ugliness score after modifying it with some number of operations.

However, as his histogram is very large, Little Dormi is having trouble minimizing the ugliness score, so as Little Dormi's older brother, help him find the minimal ugliness.

Consider the following example where the histogram has $4$ columns of heights $4,8,9,6$ :

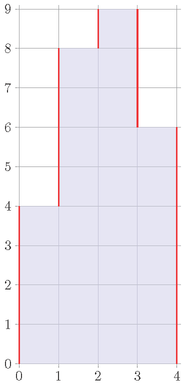The blue region represents the histogram, and the red lines represent the vertical portion of the outline. Currently, the vertical length of the outline is $4+4+1+3+6 = 18$ , so if Little Dormi does not modify the histogram at all, the ugliness would be $18$ .

However, Little Dormi can apply the operation once on column $2$ and twice on column $3$ , resulting in a histogram with heights $4,7,7,6$ :

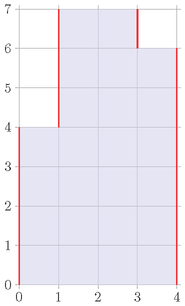Now, as the total vertical length of the outline (red lines) is $4+3+1+6=14$ , the ugliness is $14+3=17$ dollars. It can be proven that this is optimal.

Each test contains multiple test cases. The first line contains the number of test cases $t$ ( $1 \le t \le 10^4$ ). Description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $1 \le n \le 4 \cdot 10^5$ ).

The second line of each test case contains $n$ integers $a_1, a_2, \ldots, a_n$ ( $0 \le a_i \le 10^9$ ).

It is guaranteed that the sum of $n$ over all test cases does not exceed $4 \cdot 10^5$ .

For each test case output one integer, the minimal ugliness Little Dormi can achieve with the histogram in that test case.

Example $1$ is the example described in the statement.

The initial histogram for example $2$ is given below:

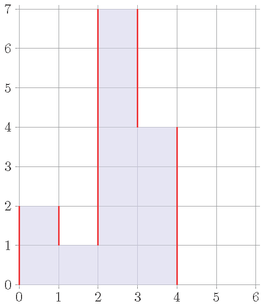The ugliness is currently $2+1+6+3+4=16$ .

By applying the operation once on column $1$ , six times on column $3$ , and three times on column $4$ , we can end up with a histogram with heights $1,1,1,1,0,0$ :

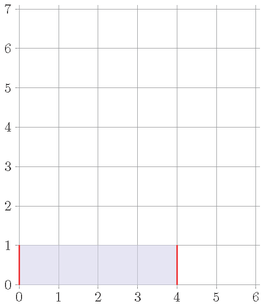The vertical length of the outline is now $1+1=2$ and Little Dormi made $1+6+3=10$ operations, so the final ugliness is $2+10=12$ , which can be proven to be optimal.