CF1537F.Figure Fixing

You have a connected undirected graph made of $n$ nodes and $m$ edges. The $i$ -th node has a value $v_i$ and a target value $t_i$ .

In an operation, you can choose an edge $(i, j)$ and add $k$ to both $v_i$ and $v_j$ , where $k$ can be any integer. In particular, $k$ can be negative.

Your task to determine if it is possible that by doing some finite number of operations (possibly zero), you can achieve for every node $i$ , $v_i = t_i$ .

The first line contains a single integer $t$ ( $1 \leq t \leq 1000$ ), the number of test cases. Then the test cases follow.

The first line of each test case contains two integers $n$ , $m$ ( $2 \leq n \leq 2\cdot 10^5$ , $n-1\leq m\leq \min(2\cdot 10^5, \frac{n(n-1)}{2})$ ) — the number of nodes and edges respectively.

The second line contains $n$ integers $v_1\ldots, v_n$ ( $-10^9 \leq v_i \leq 10^9$ ) — initial values of nodes.

The third line contains $n$ integers $t_1\ldots, t_n$ ( $-10^9 \leq t_i \leq 10^9$ ) — target values of nodes.

Each of the next $m$ lines contains two integers $i$ and $j$ representing an edge between node $i$ and node $j$ ( $1 \leq i, j \leq n$ , $i\ne j$ ).

It is guaranteed that the graph is connected and there is at most one edge between the same pair of nodes.

It is guaranteed that the sum of $n$ over all testcases does not exceed $2 \cdot 10^5$ and the sum of $m$ over all testcases does not exceed $2 \cdot 10^5$ .

For each test case, if it is possible for every node to reach its target after some number of operations, print "YES". Otherwise, print "NO".

Here is a visualization of the first test case (the orange values denote the initial values and the blue ones the desired values):

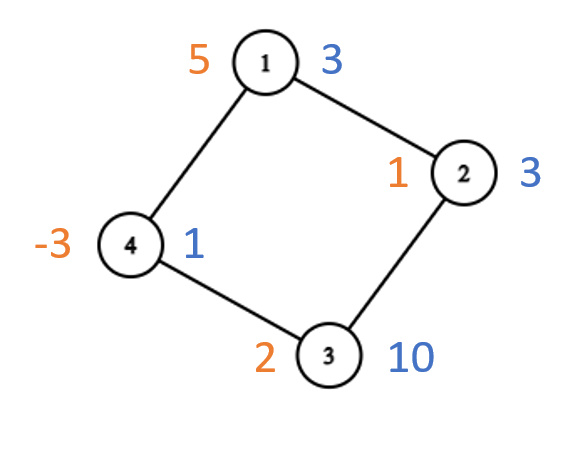One possible order of operations to obtain the desired values for each node is the following:

• Operation $1$ : Add $2$ to nodes $2$ and $3$ .
• Operation $2$ : Add $-2$ to nodes $1$ and $4$ .
• Operation $3$ : Add $6$ to nodes $3$ and $4$ .

Now we can see that in total we added $-2$ to node $1$ , $2$ to node $2$ , $8$ to node $3$ and $4$ to node $4$ which brings each node exactly to it's desired value.

For the graph from the second test case it's impossible to get the target values.