CF1501B.Napoleon Cake

This week Arkady wanted to cook some pancakes (to follow ancient traditions) and make a problem about that. But then he remembered that one can't make a problem about stacking pancakes without working at a specific IT company, so he decided to bake the Napoleon cake instead.

To bake a Napoleon cake, one has to bake $n$ dry layers first, and then put them on each other in one stack, adding some cream. Arkady started with an empty plate, and performed the following steps $n$ times:

• place a new cake layer on the top of the stack;
• after the $i$ -th layer is placed, pour $a_i$ units of cream on top of the stack.

When $x$ units of cream are poured on the top of the stack, top $x$ layers of the cake get drenched in the cream. If there are less than $x$ layers, all layers get drenched and the rest of the cream is wasted. If $x = 0$ , no layer gets drenched.

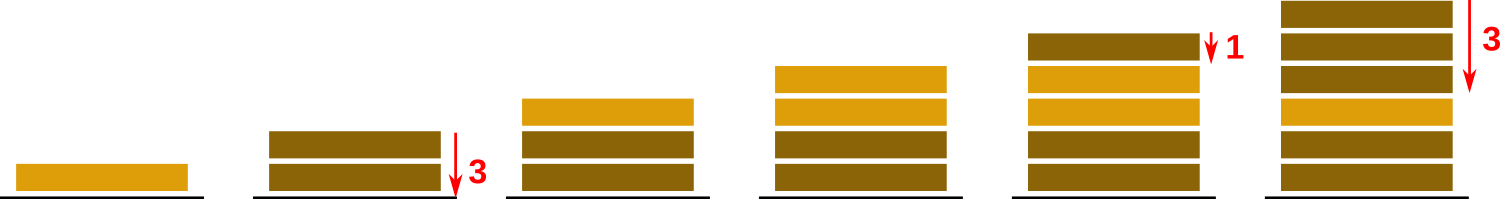The picture represents the first test case of the example.Help Arkady determine which layers of the cake eventually get drenched when the process is over, and which don't.

Each test contains multiple test cases. The first line contains the number of test cases $t$ ( $1 \le t \le 20\,000$ ). Description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $1 \le n \le 2 \cdot 10^5$ ) — the number of layers in the cake.

The second line of each test case contains $n$ integers $a_1, a_2, \ldots, a_n$ ( $0 \le a_i \le n$ ) — the amount of cream poured on the cake after adding each layer.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$ .

For each test case, print a single line with $n$ integers. The $i$ -th of the integers should be equal to $1$ if the $i$ -th layer from the bottom gets drenched, and $0$ otherwise.