CF1495F.Squares

There are $n$ squares drawn from left to right on the floor. The $i$ -th square has three integers $p_i,a_i,b_i$ , written on it. The sequence $p_1,p_2,\dots,p_n$ forms a permutation.

Each round you will start from the leftmost square $1$ and jump to the right. If you are now on the $i$ -th square, you can do one of the following two operations:

1. Jump to the $i+1$ -th square and pay the cost $a_i$ . If $i=n$ , then you can end the round and pay the cost $a_i$ .
2. Jump to the $j$ -th square and pay the cost $b_i$ , where $j$ is the leftmost square that satisfies $j > i, p_j > p_i$ . If there is no such $j$ then you can end the round and pay the cost $b_i$ .

There are $q$ rounds in the game. To make the game more difficult, you need to maintain a square set $S$ (initially it is empty). You must pass through these squares during the round (other squares can also be passed through). The square set $S$ for the $i$ -th round is obtained by adding or removing a square from the square set for the $(i-1)$ -th round.

For each round find the minimum cost you should pay to end it.

The first line contains two integers $n$ , $q$ ( $1\le n,q\le 2 \cdot 10^5$ ) — the number of squares and the number of rounds.

The second line contains $n$ distinct integers $p_1,p_2,\dots,p_n$ ( $1\le p_i\le n$ ). It is guaranteed that the sequence $p_1,p_2,\dots,p_n$ forms a permutation.

The third line contains $n$ integers $a_1,a_2,\ldots,a_n$ ( $-10^9\le a_i\le 10^9$ ).

The fourth line contains $n$ integers $b_1,b_2,\dots,b_n$ ( $-10^9\le b_i\le 10^9$ ).

Then $q$ lines follow, $i$ -th of them contains a single integer $x_i$ ( $1\le x_i\le n$ ). If $x_i$ was in the set $S$ on the $(i-1)$ -th round you should remove it, otherwise, you should add it.

Print $q$ lines, each of them should contain a single integer — the minimum cost you should pay to end the corresponding round.

Let's consider the character $T$ as the end of a round. Then we can draw two graphs for the first and the second test.

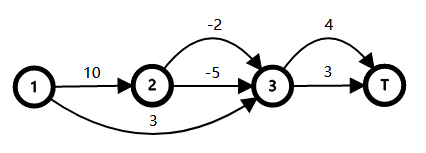
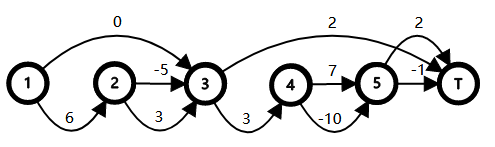In the first round of the first test, the set that you must pass through is $\{1\}$ . The path you can use is $1\to 3\to T$ and its cost is $6$ .

In the second round of the first test, the set that you must pass through is $\{1,2\}$ . The path you can use is $1\to 2\to 3\to T$ and its cost is $8$ .