CF1450H2.Multithreading (Hard Version)

The only difference between the two versions of the problem is that there are no updates in the easy version.

There are $n$ spools of thread placed on the rim of a circular table. The spools come in two types of thread: the first thread is black and the second thread is white.

For any two spools of the same color, you can attach them with a thread of that color in a straight line segment. Define a matching as a way to attach spools together so that each spool is attached to exactly one other spool.

Coloring is an assignment of colors (white and black) to the spools. A coloring is called valid if it has at least one matching. That is if the number of black spools and the number of white spools are both even.

Given a matching, we can find the number of times some white thread intersects some black thread. We compute the number of pairs of differently colored threads that intersect instead of the number of intersection points, so one intersection point may be counted multiple times if different pairs of threads intersect at the same point. If $c$ is a valid coloring, let $f(c)$ denote the minimum number of such intersections out of all possible matchings.

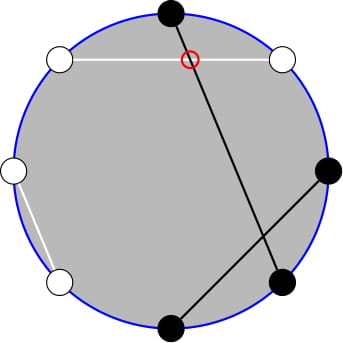The circle above is described by the coloring bwbbbwww. After matching the spools as shown, there is one intersection between differently colored threads. It can be proven that it is the minimum possible, so $f(\text{bwbbbwww}) = 1$ . You are given a string $s$ representing an unfinished coloring, with black, white, and uncolored spools. A coloring $c$ is called $s$ -reachable if you can achieve it by assigning colors to the uncolored spools of $s$ without changing the others.

A coloring $c$ is chosen uniformly at random among all valid, $s$ -reachable colorings. Compute the expected value of $f(c)$ . You should find it by modulo $998244353$ .

There will be $m$ updates to change one character of $s$ . After each update, you should again compute the expected value of $f(c)$ .

We can show that each answer can be written in the form $\frac{p}{q}$ where $p$ and $q$ are relatively prime integers and $q\not\equiv 0\pmod{998244353}$ . The answer by modulo $998244353$ is equal to $(p\cdot q^{-1})$ modulo $998244353$ .

The first line contains two integers $n$ , $m$ ( $2\le n\le 2\cdot 10^5$ , $n$ is even, $0\le m\le 2\cdot 10^5$ ) — the number of spools and the number of updates, respectively.

The second line contains a string $s$ of length $n$ — the unfinished coloring of the spools. The $i$ -th character will be 'w', 'b', or '?', describing if the $i$ -th spool is white, black, or uncolored, respectively.

Each of the next $m$ lines contains an integer $i$ ( $1 \leq i \leq n$ ) — the position of the character in $s$ to be updated, and a character $c$ ( $c \in \{\text{w}, \text{b}, \text{?}\}$ ) — the new color of the spool $i$ after the update.

It is guaranteed there exists at least one uncolored spool initially and after each update.

Print $m+1$ lines: the expected value of $f(c)$ initially and after each update. All values should be found by modulo $998244353$ .

The first test corresponds closely to the image. Coloring '?' as 'w' does not create a valid coloring because the number of black spools is odd. Then the only reachable valid coloring is 'bwbbbwww' and $f(\text{bwbbbwww}) = 1$ , so the expected value is $1$ .

In the second test, the string after each update is:

1. ????w?wb??
2. ??????wb??
3. ?w????wb??

In the third test, the string after each update is:

1. ww?b
2. wb?b
3. wb?b