CF1433G.Reducing Delivery Cost

You are a mayor of Berlyatov. There are $n$ districts and $m$ two-way roads between them. The $i$ -th road connects districts $x_i$ and $y_i$ . The cost of travelling along this road is $w_i$ . There is some path between each pair of districts, so the city is connected.

There are $k$ delivery routes in Berlyatov. The $i$ -th route is going from the district $a_i$ to the district $b_i$ . There is one courier on each route and the courier will always choose the cheapest (minimum by total cost) path from the district $a_i$ to the district $b_i$ to deliver products.

The route can go from the district to itself, some couriers routes can coincide (and you have to count them independently).

You can make at most one road to have cost zero (i.e. you choose at most one road and change its cost with $0$ ).

Let $d(x, y)$ be the cheapest cost of travel between districts $x$ and $y$ .

Your task is to find the minimum total courier routes cost you can achieve, if you optimally select the some road and change its cost with $0$ . In other words, you have to find the minimum possible value of $\sum\limits_{i = 1}^{k} d(a_i, b_i)$ after applying the operation described above optimally.

The first line of the input contains three integers $n$ , $m$ and $k$ ( $2 \le n \le 1000$ ; $n - 1 \le m \le min(1000, \frac{n(n-1)}{2})$ ; $1 \le k \le 1000$ ) — the number of districts, the number of roads and the number of courier routes.

The next $m$ lines describe roads. The $i$ -th road is given as three integers $x_i$ , $y_i$ and $w_i$ ( $1 \le x_i, y_i \le n$ ; $x_i \ne y_i$ ; $1 \le w_i \le 1000$ ), where $x_i$ and $y_i$ are districts the $i$ -th road connects and $w_i$ is its cost. It is guaranteed that there is some path between each pair of districts, so the city is connected. It is also guaranteed that there is at most one road between each pair of districts.

The next $k$ lines describe courier routes. The $i$ -th route is given as two integers $a_i$ and $b_i$ ( $1 \le a_i, b_i \le n$ ) — the districts of the $i$ -th route. The route can go from the district to itself, some couriers routes can coincide (and you have to count them independently).

Print one integer — the minimum total courier routes cost you can achieve (i.e. the minimum value $\sum\limits_{i=1}^{k} d(a_i, b_i)$ , where $d(x, y)$ is the cheapest cost of travel between districts $x$ and $y$ ) if you can make some (at most one) road cost zero.

The picture corresponding to the first example:

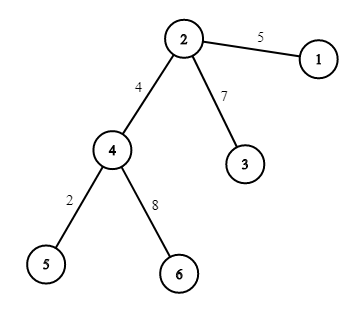
There, you can choose either the road $(2, 4)$ or the road $(4, 6)$ . Both options lead to the total cost $22$ .

The picture corresponding to the second example:

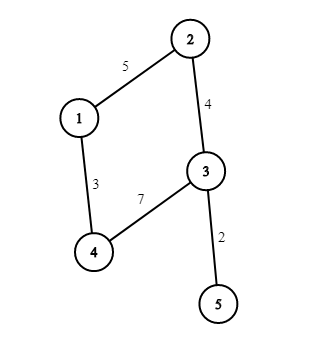
There, you can choose the road $(3, 4)$ . This leads to the total cost $13$ .