CF1394E.Boboniu and Banknote Collection

No matter what trouble you're in, don't be afraid, but face it with a smile.

I've made another billion dollars!

— Boboniu

Boboniu has issued his currencies, named Bobo Yuan. Bobo Yuan (BBY) is a series of currencies. Boboniu gives each of them a positive integer identifier, such as BBY-1, BBY-2, etc.

Boboniu has a BBY collection. His collection looks like a sequence. For example:

We can use sequence $a=[1,2,3,3,2,1,4,4,1]$ of length $n=9$ to denote it.

Now Boboniu wants to fold his collection. You can imagine that Boboniu stick his collection to a long piece of paper and fold it between currencies:

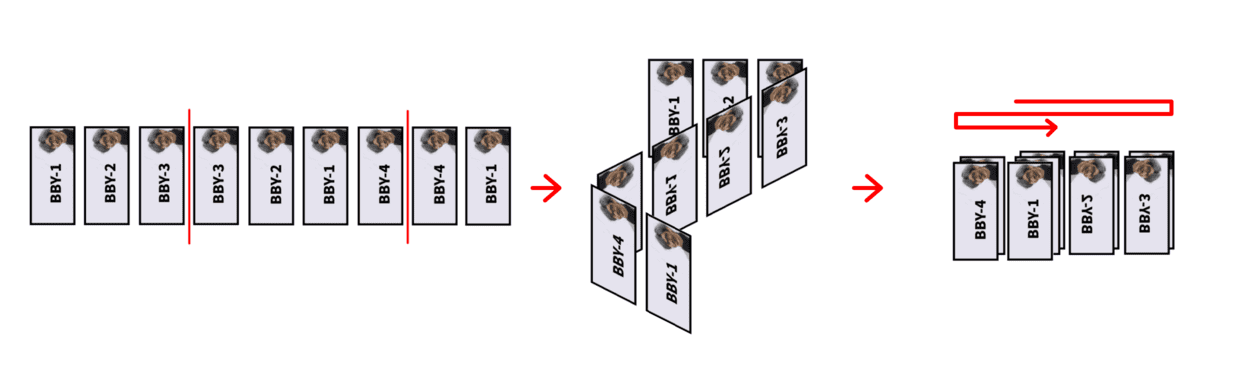Boboniu will only fold the same identifier of currencies together. In other words, if $a_i$ is folded over $a_j$ ( $1\le i,j\le n$ ), then $a_i=a_j$ must hold. Boboniu doesn't care if you follow this rule in the process of folding. But once it is finished, the rule should be obeyed.

A formal definition of fold is described in notes.

According to the picture above, you can fold $a$ two times. In fact, you can fold $a=[1,2,3,3,2,1,4,4,1]$ at most two times. So the maximum number of folds of it is $2$ .

As an international fan of Boboniu, you're asked to calculate the maximum number of folds.

You're given a sequence $a$ of length $n$ , for each $i$ ( $1\le i\le n$ ), you need to calculate the maximum number of folds of $[a_1,a_2,\ldots,a_i]$ .

The first line contains an integer $n$ ( $1\le n\le 10^5$ ).

The second line contains $n$ integers $a_1,a_2,\ldots,a_n$ ( $1\le a_i\le n$ ).

Print $n$ integers. The $i$ -th of them should be equal to the maximum number of folds of $[a_1,a_2,\ldots,a_i]$ .

Formally, for a sequence $a$ of length $n$ , let's define the folding sequence as a sequence $b$ of length $n$ such that:

• $b_i$ ( $1\le i\le n$ ) is either $1$ or $-1$ .
• Let $p(i)=[b_i=1]+\sum_{j=1}^{i-1}b_j$ . For all $1\le i<j\le n$ , if $p(i)=p(j)$ , then $a_i$ should be equal to $a_j$ .

( $[A]$ is the value of boolean expression $A$ . i. e. $[A]=1$ if $A$ is true, else $[A]=0$ ).

Now we define the number of folds of $b$ as $f(b)=\sum_{i=1}^{n-1}[b_i\ne b_{i+1}]$ .

The maximum number of folds of $a$ is $F(a)=\max\{ f(b)\mid b \text{ is a folding sequence of }a \}$ .