CF1409E.Two Platforms

There are $n$ points on a plane. The $i$ -th point has coordinates $(x_i, y_i)$ . You have two horizontal platforms, both of length $k$ . Each platform can be placed anywhere on a plane but it should be placed horizontally (on the same $y$ -coordinate) and have integer borders. If the left border of the platform is $(x, y)$ then the right border is $(x + k, y)$ and all points between borders (including borders) belong to the platform.

Note that platforms can share common points (overlap) and it is not necessary to place both platforms on the same $y$ -coordinate.

When you place both platforms on a plane, all points start falling down decreasing their $y$ -coordinate. If a point collides with some platform at some moment, the point stops and is saved. Points which never collide with any platform are lost.

Your task is to find the maximum number of points you can save if you place both platforms optimally.

You have to answer $t$ independent test cases.

For better understanding, please read the Note section below to see a picture for the first test case.

The first line of the input contains one integer $t$ ( $1 \le t \le 2 \cdot 10^4$ ) — the number of test cases. Then $t$ test cases follow.

The first line of the test case contains two integers $n$ and $k$ ( $1 \le n \le 2 \cdot 10^5$ ; $1 \le k \le 10^9$ ) — the number of points and the length of each platform, respectively. The second line of the test case contains $n$ integers $x_1, x_2, \dots, x_n$ ( $1 \le x_i \le 10^9$ ), where $x_i$ is $x$ -coordinate of the $i$ -th point. The third line of the input contains $n$ integers $y_1, y_2, \dots, y_n$ ( $1 \le y_i \le 10^9$ ), where $y_i$ is $y$ -coordinate of the $i$ -th point. All points are distinct (there is no pair $1 \le i < j \le n$ such that $x_i = x_j$ and $y_i = y_j$ ).

It is guaranteed that the sum of $n$ does not exceed $2 \cdot 10^5$ ( $\sum n \le 2 \cdot 10^5$ ).

For each test case, print the answer: the maximum number of points you can save if you place both platforms optimally.

The picture corresponding to the first test case of the example:

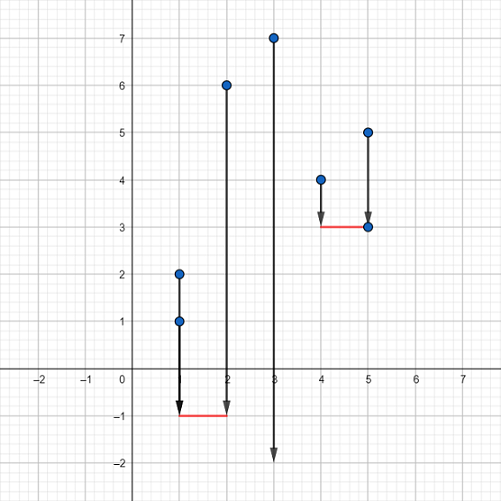
Blue dots represent the points, red segments represent the platforms. One of the possible ways is to place the first platform between points $(1, -1)$ and $(2, -1)$ and the second one between points $(4, 3)$ and $(5, 3)$ . Vectors represent how the points will fall down. As you can see, the only point we can't save is the point $(3, 7)$ so it falls down infinitely and will be lost. It can be proven that we can't achieve better answer here. Also note that the point $(5, 3)$ doesn't fall at all because it is already on the platform.