CF1372E.Omkar and Last Floor

Omkar is building a house. He wants to decide how to make the floor plan for the last floor.

Omkar's floor starts out as $n$ rows of $m$ zeros ( $1 \le n,m \le 100$ ). Every row is divided into intervals such that every $0$ in the row is in exactly $1$ interval. For every interval for every row, Omkar can change exactly one of the $0$ s contained in that interval to a $1$ . Omkar defines the quality of a floor as the sum of the squares of the sums of the values in each column, i. e. if the sum of the values in the $i$ -th column is $q_i$ , then the quality of the floor is $\sum_{i = 1}^m q_i^2$ .

Help Omkar find the maximum quality that the floor can have.

The first line contains two integers, $n$ and $m$ ( $1 \le n,m \le 100$ ), which are the number of rows and number of columns, respectively.

You will then receive a description of the intervals in each row. For every row $i$ from $1$ to $n$ : The first row contains a single integer $k_i$ ( $1 \le k_i \le m$ ), which is the number of intervals on row $i$ . The $j$ -th of the next $k_i$ lines contains two integers $l_{i,j}$ and $r_{i,j}$ , which are the left and right bound (both inclusive), respectively, of the $j$ -th interval of the $i$ -th row. It is guaranteed that all intervals other than the first interval will be directly after the interval before it. Formally, $l_{i,1} = 1$ , $l_{i,j} \leq r_{i,j}$ for all $1 \le j \le k_i$ , $r_{i,j-1} + 1 = l_{i,j}$ for all $2 \le j \le k_i$ , and $r_{i,k_i} = m$ .

Output one integer, which is the maximum possible quality of an eligible floor plan.

The given test case corresponds to the following diagram. Cells in the same row and have the same number are a part of the same interval.

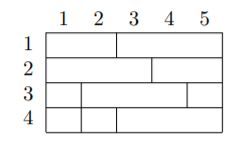The most optimal assignment is:

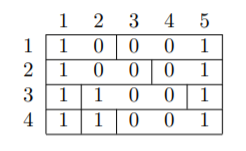The sum of the $1$ st column is $4$ , the sum of the $2$ nd column is $2$ , the sum of the $3$ rd and $4$ th columns are $0$ , and the sum of the $5$ th column is $4$ .

The quality of this floor plan is $4^2 + 2^2 + 0^2 + 0^2 + 4^2 = 36$ . You can show that there is no floor plan with a higher quality.