CF1363E.Tree Shuffling

Ashish has a tree consisting of $n$ nodes numbered $1$ to $n$ rooted at node $1$ . The $i$ -th node in the tree has a cost $a_i$ , and binary digit $b_i$ is written in it. He wants to have binary digit $c_i$ written in the $i$ -th node in the end.

To achieve this, he can perform the following operation any number of times:

• Select any $k$ nodes from the subtree of any node $u$ , and shuffle the digits in these nodes as he wishes, incurring a cost of $k \cdot a_u$ . Here, he can choose $k$ ranging from $1$ to the size of the subtree of $u$ .

He wants to perform the operations in such a way that every node finally has the digit corresponding to its target.

Help him find the minimum total cost he needs to spend so that after all the operations, every node $u$ has digit $c_u$ written in it, or determine that it is impossible.

First line contains a single integer $n$ $(1 \le n \le 2 \cdot 10^5)$ denoting the number of nodes in the tree.

$i$ -th line of the next $n$ lines contains 3 space-separated integers $a_i$ , $b_i$ , $c_i$ $(1 \leq a_i \leq 10^9, 0 \leq b_i, c_i \leq 1)$ — the cost of the $i$ -th node, its initial digit and its goal digit.

Each of the next $n - 1$ lines contain two integers $u$ , $v$ $(1 \leq u, v \leq n, \text{ } u \ne v)$ , meaning that there is an edge between nodes $u$ and $v$ in the tree.

Print the minimum total cost to make every node reach its target digit, and $-1$ if it is impossible.

The tree corresponding to samples $1$ and $2$ are:

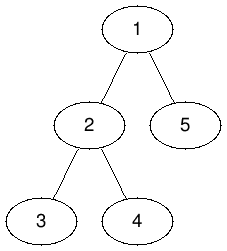In sample $1$ , we can choose node $1$ and $k = 4$ for a cost of $4 \cdot 1$ = $4$ and select nodes ${1, 2, 3, 5}$ , shuffle their digits and get the desired digits in every node.

In sample $2$ , we can choose node $1$ and $k = 2$ for a cost of $10000 \cdot 2$ , select nodes ${1, 5}$ and exchange their digits, and similarly, choose node $2$ and $k = 2$ for a cost of $2000 \cdot 2$ , select nodes ${2, 3}$ and exchange their digits to get the desired digits in every node.

In sample $3$ , it is impossible to get the desired digits, because there is no node with digit $1$ initially.