CF1324F.Maximum White Subtree

You are given a tree consisting of $n$ vertices. A tree is a connected undirected graph with $n-1$ edges. Each vertex $v$ of this tree has a color assigned to it ( $a_v = 1$ if the vertex $v$ is white and $0$ if the vertex $v$ is black).

You have to solve the following problem for each vertex $v$ : what is the maximum difference between the number of white and the number of black vertices you can obtain if you choose some subtree of the given tree that contains the vertex $v$ ? The subtree of the tree is the connected subgraph of the given tree. More formally, if you choose the subtree that contains $cnt_w$ white vertices and $cnt_b$ black vertices, you have to maximize $cnt_w - cnt_b$ .
给你一棵由 $n$ 个顶点组成的树。树是一个有 $n-1$ 条边的连通无向图。这棵树的每个顶点 $v$ 都有一种颜色（如果顶点 $v$ 是白色，则颜色为 $a_v = 1$ ；如果顶点 $v$ 是黑色，则颜色为 $0$ ）。

对于每个顶点 $v$ 你都必须解决下面的问题：如果从给定的树中选择一棵包含顶点 $v$ 的子树，那么白色顶点的数量和黑色顶点的数量之间的最大差是多少？树的子树是给定树的连接子图。更具体地说，如果选择包含 $cnt_w$ 个白色顶点和 $cnt_b$ 个黑色顶点的子树，则必须最大化 $cnt_w - cnt_b$ 。

The first line of the input contains one integer $n$ ( $2 \le n \le 2 \cdot 10^5$ ) — the number of vertices in the tree.

The second line of the input contains $n$ integers $a_1, a_2, \dots, a_n$ ( $0 \le a_i \le 1$ ), where $a_i$ is the color of the $i$ -th vertex.

Each of the next $n-1$ lines describes an edge of the tree. Edge $i$ is denoted by two integers $u_i$ and $v_i$ , the labels of vertices it connects $(1 \le u_i, v_i \le n, u_i \ne v_i$ ).

It is guaranteed that the given edges form a tree.
输入

输入的第一行包含一个整数 $n$ （ $2 \le n \le 2 \cdot 10^5$ ）。( $2 \le n \le 2 \cdot 10^5$ ) - 树的顶点数。

第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$ ( $0 \le a_i \le 1$ )，其中 $a_i$ 是第 $i$ 个顶点的颜色。

接下来的每一行 $n-1$ 都描述了树的一条边。边 $i$ 由两个整数 $u_i$ 和 $v_i$ 表示，它连接的顶点的标签为 $(1 \le u_i, v_i \le n, u_i \ne v_i$ ）。

可以保证给定的边构成一棵树。

Print $n$ integers $res_1, res_2, \dots, res_n$ , where $res_i$ is the maximum possible difference between the number of white and black vertices in some subtree that contains the vertex $i$ .
输出

打印 $n$ 个整数 $res_1, res_2, \dots, res_n$ ，其中 $res_i$ 是包含顶点 $i$ 的某个子树上白色顶点和黑色顶点数量的最大可能差值。

The first example is shown below:

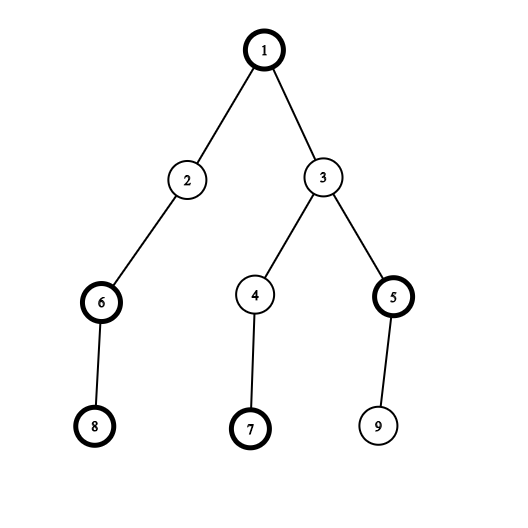
The black vertices have bold borders.

In the second example, the best subtree for vertices $2, 3$ and $4$ are vertices $2, 3$ and $4$ correspondingly. And the best subtree for the vertex $1$ is the subtree consisting of vertices $1$ and $3$ .
备注

第一个示例如图所示：

黑色顶点有粗体边框。

在第二个例子中，顶点 $2, 3$ 和 $4$ 的最佳子树分别是顶点 $2, 3$ 和 $4$ 。而顶点 $1$ 的最佳子树是由顶点 $1$ 和 $3$ 组成的子树。