CF1282E.The Cake Is a Lie

We are committed to the well being of all participants. Therefore, instead of the problem, we suggest you enjoy a piece of cake.

Uh oh. Somebody cut the cake. We told them to wait for you, but they did it anyway. There is still some left, though, if you hurry back. Of course, before you taste the cake, you thought about how the cake was cut.

It is known that the cake was originally a regular $n$ -sided polygon, each vertex of which had a unique number from $1$ to $n$ . The vertices were numbered in random order.

Each piece of the cake is a triangle. The cake was cut into $n - 2$ pieces as follows: each time one cut was made with a knife (from one vertex to another) such that exactly one triangular piece was separated from the current cake, and the rest continued to be a convex polygon. In other words, each time three consecutive vertices of the polygon were selected and the corresponding triangle was cut off.

A possible process of cutting the cake is presented in the picture below.

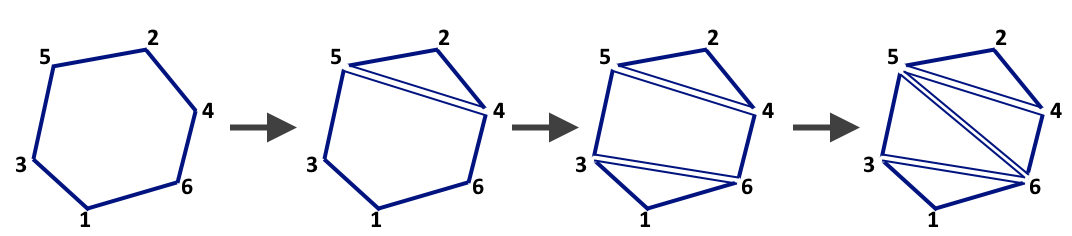Example of 6-sided cake slicing.You are given a set of $n-2$ triangular pieces in random order. The vertices of each piece are given in random order — clockwise or counterclockwise. Each piece is defined by three numbers — the numbers of the corresponding $n$ -sided cake vertices.

For example, for the situation in the picture above, you could be given a set of pieces: $[3, 6, 5], [5, 2, 4], [5, 4, 6], [6, 3, 1]$ .

You are interested in two questions.

• What was the enumeration of the $n$ -sided cake vertices?
• In what order were the pieces cut?

Formally, you have to find two permutations $p_1, p_2, \dots, p_n$ ( $1 \le p_i \le n$ ) and $q_1, q_2, \dots, q_{n - 2}$ ( $1 \le q_i \le n - 2$ ) such that if the cake vertices are numbered with the numbers $p_1, p_2, \dots, p_n$ in order clockwise or counterclockwise, then when cutting pieces of the cake in the order $q_1, q_2, \dots, q_{n - 2}$ always cuts off a triangular piece so that the remaining part forms one convex polygon.

For example, in the picture above the answer permutations could be: $p=[2, 4, 6, 1, 3, 5]$ (or any of its cyclic shifts, or its reversal and after that any cyclic shift) and $q=[2, 4, 1, 3]$ .

Write a program that, based on the given triangular pieces, finds any suitable permutations $p$ and $q$ .

The first line contains a single integer $t$ ( $1 \le t \le 1000$ ) — the number of test cases. Then there are $t$ independent sets of input data.

The first line of each set consists of a single integer $n$ ( $3 \le n \le 10^5$ ) — the number of vertices in the cake.

The following $n - 2$ lines describe the numbers of the pieces vertices: each line consists of three different integers $a, b, c$ ( $1 \le a, b, c \le n$ ) — the numbers of the pieces vertices of cake given in random order. The pieces are given in random order.

It is guaranteed that the answer to each of the tests exists. It is also guaranteed that the sum of $n$ for all test cases does not exceed $10^5$ .

Print $2t$ lines — answers to given $t$ test cases in the order in which they are written in the input. Each answer should consist of $2$ lines.

In the first line of an answer on a test case print $n$ distinct numbers $p_1, p_2, \dots, p_n$ ( $1 \le p_i \le n$ ) — the numbers of the cake vertices in clockwise or counterclockwise order.

In the second line of an answer on a test case print $n - 2$ distinct numbers $q_1, q_2, \dots, q_{n - 2}$ ( $1 \le q_i \le n - 2$ ) — the order of cutting pieces of the cake. The number of a piece of the cake corresponds to its number in the input.

If there are several answers, print any. It is guaranteed that the answer to each of the tests exists.