CF1252I.Mission Possible

Input begins with a line containing five integers: $N$ $x_L$ $y_L$ $x_R$ $y_R$ ( $0 \le N \le 50$ ; $0 \le x_L < x_R \le 1000$ ; $0 \le y_L < y_R \le 1000$ ) representing the number of sensors and the secret base ( $x_L$ , $y_L$ , $x_R$ , $y_R$ ), respectively. The next line contains two integers: $x_s$ $y_s$ ( $x_L < x_s < x_R$ ; $y_L < y_s < y_R$ ) representing Allen's initial location. The next line contains two integers: $x_t$ $y_t$ ( $x_L < x_t < x_R$ ; $y_L < y_t < y_R$ ) representing Allen's target location. It is guaranteed that $x_s \ne x_t$ or $y_s \ne y_t$ . The next $N$ lines each contains three integers: $x_i$ $y_i$ $r_i$ ( $x_L < x_i - r_i < x_i + r_i < x_R$ ; $y_L < y_i - r_i < y_i + r_i < y_R$ ; $1 \le r_i \le 1000$ ) representing a sensor at location $(x_i, y_i)$ with an effective sensing radius of $r_i$ . It is guaranteed that the Euclidean distance of any two sensors $i$ and $j$ is larger than $r_i + r_j$ . It is also guaranteed that the Euclidean distance of $(x_s,y_s)$ and $(x_t,y_t)$ to any sensor $i$ is larger than $r_i$ .

Output in a line an integer representing the size of a feasible $P$ . The next $|P|$ lines each contains two real numbers (separated by a single space); the $j^{th}$ line contains $x_j$ $y_j$ representing the $j^{th}$ point in $P$ . You may output any feasible $P$ with no more than $1000$ points.

Due to the nature of the output (floating point), let us define an epsilon $\epsilon$ to be $10^{-6}$ to verify the output. Consider $Q_1 = (x_s, y_s)$ , $Q_{j+1} = P_j$ for all $1 \le j \le |P|$ , and $Q_{|P|+2} = (x_t, y_t)$ . Then, $P$ is considered correct if and only if $P$ contains no more than $1000$ points and all of the following are satisfied:

• $x_L - \epsilon \le x_{p_k} \le x_R + \epsilon$ and $y_L - \epsilon \le y_{p_k} \le y_R + \epsilon$ for all $1 \le k \le |P|$ (Allen is not running out of the secret base).
• For all $1 \le k < |Q|$ , let $S_k$ be the line segment connecting $Q_k$ and $Q_{k+1}$ (Allen is running in straight line). For all $1 \le i \le N$ , let $(x_{k,i},y_{k,i})$ be the point along $S_k$ that is the closest to the $i^{th}$ sensor's location, $(x_i,y_i)$ . Let $d_{k,i}$ be the Euclidean distance between $(x_{k,i},y_{k,i})$ and $(x_i,y_i)$ . Then, the constraint $r_i \le d_{k,i} + \epsilon$ should be satisfied (Allen is not detected by any sensor).
• All points in $Q$ are distinct. Two points, $(x_a,y_a)$ and $(x_b,y_b)$ , are considered distinct if and only if $|x_a - x_b| > \epsilon$ or $|y_a - y_b| > \epsilon$ .

Explanation for the sample input/output #1

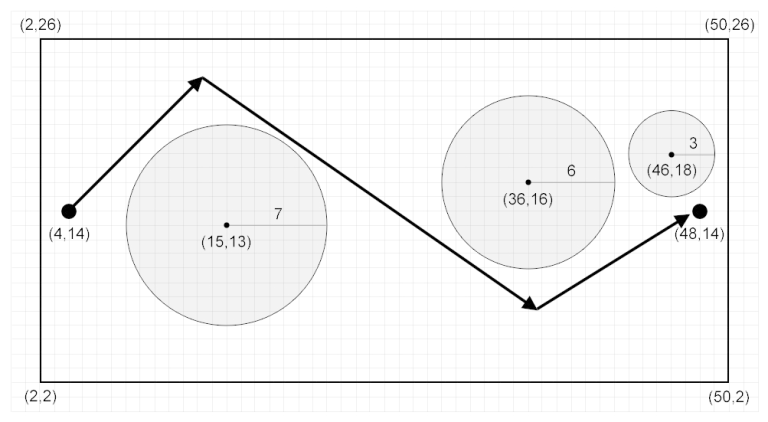
The figure above shows the $P$ from the sample output. Note that there exists a feasible $P$ with only one point in this sample, although you are not required to find such $P$ .

Explanation for the sample input/output #1

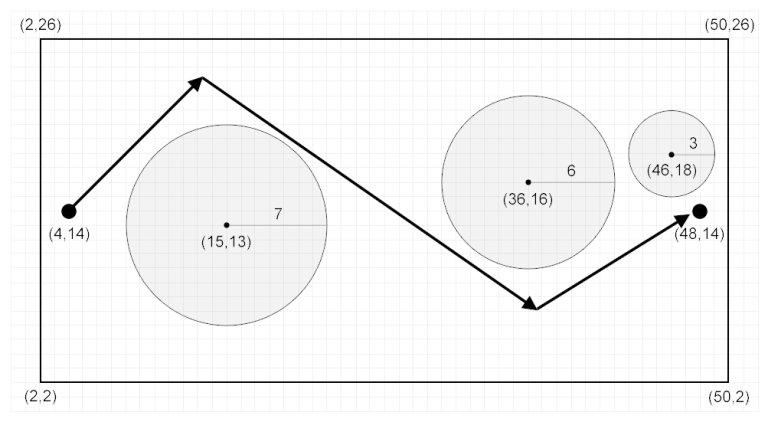
The figure above shows the $P$ from the sample output. Note that there exists a feasible $P$ with only one point in this sample, although you are not required to find such $P$ .