CF1253F.Cheap Robot

You're given a simple, undirected, connected, weighted graph with $n$ nodes and $m$ edges.

Nodes are numbered from $1$ to $n$ . There are exactly $k$ centrals (recharge points), which are nodes $1, 2, \ldots, k$ .

We consider a robot moving into this graph, with a battery of capacity $c$ , not fixed by the constructor yet. At any time, the battery contains an integer amount $x$ of energy between $0$ and $c$ inclusive.

Traversing an edge of weight $w_i$ is possible only if $x \ge w_i$ , and costs $w_i$ energy points ( $x := x - w_i$ ).

Moreover, when the robot reaches a central, its battery is entirely recharged ( $x := c$ ).

You're given $q$ independent missions, the $i$ -th mission requires to move the robot from central $a_i$ to central $b_i$ .

For each mission, you should tell the minimum capacity required to acheive it.

The first line contains four integers $n$ , $m$ , $k$ and $q$ ( $2 \le k \le n \le 10^5$ and $1 \le m, q \le 3 \cdot 10^5$ ).

The $i$ -th of the next $m$ lines contains three integers $u_i$ , $v_i$ and $w_i$ ( $1 \le u_i, v_i \le n$ , $u_i \neq v_i$ , $1 \le w_i \le 10^9$ ), that mean that there's an edge between nodes $u$ and $v$ , with a weight $w_i$ .

It is guaranteed that the given graph is simple (there is no self-loop, and there is at most one edge between every pair of nodes) and connected.

The $i$ -th of the next $q$ lines contains two integers $a_i$ and $b_i$ ( $1 \le a_i, b_i \le k$ , $a_i \neq b_i$ ).

You have to output $q$ lines, where the $i$ -th line contains a single integer : the minimum capacity required to acheive the $i$ -th mission.

In the first example, the graph is the chain $10 - 9 - 2^C - 4 - 1^C - 5 - 7 - 3^C - 8 - 6$ , where centrals are nodes $1$ , $2$ and $3$ .

For the mission $(2, 3)$ , there is only one simple path possible. Here is a simulation of this mission when the capacity is $12$ .

• The robot begins on the node $2$ , with $c = 12$ energy points.
• The robot uses an edge of weight $4$ .
• The robot reaches the node $4$ , with $12 - 4 = 8$ energy points.
• The robot uses an edge of weight $8$ .
• The robot reaches the node $1$ with $8 - 8 = 0$ energy points.
• The robot is on a central, so its battery is recharged. He has now $c = 12$ energy points.
• The robot uses an edge of weight $2$ .
• The robot is on the node $5$ , with $12 - 2 = 10$ energy points.
• The robot uses an edge of weight $3$ .
• The robot is on the node $7$ , with $10 - 3 = 7$ energy points.
• The robot uses an edge of weight $2$ .
• The robot is on the node $3$ , with $7 - 2 = 5$ energy points.
• The robot is on a central, so its battery is recharged. He has now $c = 12$ energy points.
• End of the simulation.

Note that if value of $c$ was lower than $12$ , we would have less than $8$ energy points on node $4$ , and we would be unable to use the edge $4 \leftrightarrow 1$ of weight $8$ . Hence $12$ is the minimum capacity required to acheive the mission.

—

The graph of the second example is described here (centrals are red nodes):

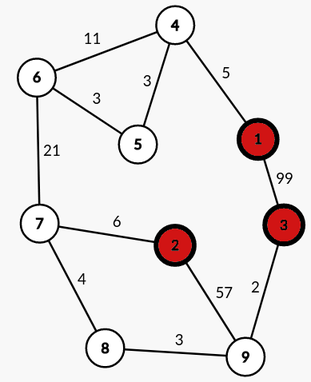The robot can acheive the mission $(3, 1)$ with a battery of capacity $c = 38$ , using the path $3 \rightarrow 9 \rightarrow 8 \rightarrow 7 \rightarrow 2 \rightarrow 7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 1$

The robot can acheive the mission $(2, 3)$ with a battery of capacity $c = 15$ , using the path $2 \rightarrow 7 \rightarrow 8 \rightarrow 9 \rightarrow 3$