CF1254D.Tree Queries

Hanh is a famous biologist. He loves growing trees and doing experiments on his own garden.

One day, he got a tree consisting of $n$ vertices. Vertices are numbered from $1$ to $n$ . A tree with $n$ vertices is an undirected connected graph with $n-1$ edges. Initially, Hanh sets the value of every vertex to $0$ .

Now, Hanh performs $q$ operations, each is either of the following types:

• Type $1$ : Hanh selects a vertex $v$ and an integer $d$ . Then he chooses some vertex $r$ uniformly at random, lists all vertices $u$ such that the path from $r$ to $u$ passes through $v$ . Hanh then increases the value of all such vertices $u$ by $d$ .
• Type $2$ : Hanh selects a vertex $v$ and calculates the expected value of $v$ .

Since Hanh is good at biology but not math, he needs your help on these operations.

The first line contains two integers $n$ and $q$ ( $1 \leq n, q \leq 150\,000$ ) — the number of vertices on Hanh's tree and the number of operations he performs.

Each of the next $n - 1$ lines contains two integers $u$ and $v$ ( $1 \leq u, v \leq n$ ), denoting that there is an edge connecting two vertices $u$ and $v$ . It is guaranteed that these $n - 1$ edges form a tree.

Each of the last $q$ lines describes an operation in either formats:

• $1$ $v$ $d$ ( $1 \leq v \leq n, 0 \leq d \leq 10^7$ ), representing a first-type operation.
• $2$ $v$ ( $1 \leq v \leq n$ ), representing a second-type operation.

It is guaranteed that there is at least one query of the second type.

For each operation of the second type, write the expected value on a single line.

Let $M = 998244353$ , it can be shown that the expected value can be expressed as an irreducible fraction $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \not \equiv 0 \pmod{M}$ . Output the integer equal to $p \cdot q^{-1} \bmod M$ . In other words, output such an integer $x$ that $0 \le x < M$ and $x \cdot q \equiv p \pmod{M}$ .

The image below shows the tree in the example:

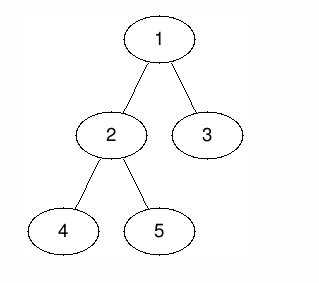For the first query, where $v = 1$ and $d = 1$ :

• If $r = 1$ , the values of all vertices get increased.
• If $r = 2$ , the values of vertices $1$ and $3$ get increased.
• If $r = 3$ , the values of vertices $1$ , $2$ , $4$ and $5$ get increased.
• If $r = 4$ , the values of vertices $1$ and $3$ get increased.
• If $r = 5$ , the values of vertices $1$ and $3$ get increased.

Hence, the expected values of all vertices after this query are ( $1, 0.4, 0.8, 0.4, 0.4$ ).

For the second query, where $v = 2$ and $d = 2$ :

• If $r = 1$ , the values of vertices $2$ , $4$ and $5$ get increased.
• If $r = 2$ , the values of all vertices get increased.
• If $r = 3$ , the values of vertices $2$ , $4$ and $5$ get increased.
• If $r = 4$ , the values of vertices $1$ , $2$ , $3$ and $5$ get increased.
• If $r = 5$ , the values of vertices $1$ , $2$ , $3$ and $4$ get increased.

Hence, the expected values of all vertices after this query are ( $2.2, 2.4, 2, 2, 2$ ).